Oxford Mathematician Neave O’Clery recently moved to Oxford from the Center for International Development at Harvard University where she worked on the development of mathematical models to describe the processes behind industrial diversification and economic growth. Here she discusses how network science can help us understand the success of cities, and provide practical tools for policy-makers.
Urban centres draw a diverse range of people, attracted by opportunity, amenities, and the energy of crowds. Yet, while benefiting from density and proximity of people, cities also suffer from issues surrounding crime, transport, housing, and education. Fuelled by rapid urbanisation and pressing policy concerns, an unparalleled inter-disciplinary research agenda has emerged that spans the humanities, social and physical sciences. From a quantitative perspective, this agenda embraces the new wave of data emerging from both the private and public sector, and its promise to deliver new insights and transformative detail on how society functions today. The novel application of tools from mathematics, combined with high resolution data, to study social, economic and physical systems transcends traditional domain boundaries and provides opportunities for a uniquely multi-disciplinary and high impact research agenda.
One particular strand of research concerns the fundamental question: how do cities move into new economic activities, providing opportunities for citizens and generating inclusive growth? Cities are naturally constrained by their current resources, and the proximity of their current capabilities to new opportunities. This simple fact gives rise to a notion of path dependence: cities move into new activities that are similar to what they currently produce. In order to describe the similarities between industries, we construct a network model where nodes represent industries and edges represent capability overlap. The capability overlap for industry pairs may be empirically estimated by counting worker transitions between industries. Intuitively, if many workers switch jobs between a pair of industries, then it is likely that these industries share a high degree of knowhow.
This network can be seen as modelling the opportunity landscape of cities: where a particular city is located in this network (i.e., its industries) will determine its future diversification potential. In other words, a city has the skills and knowhow to move into neighbouring nodes. A city located in a central well-connected region has many options, but one with only few peripheral industries has limited opportunities.
Such models aid policy-makers, planners and investors by providing detailed predictions of what types of new activities are likely to be successful in a particular place - information that typically cannot be gleaned from standard economic models. Metrics derived from such networks are informative about a range of associated questions concerning the overall growth of formal employment and the optimal size of urban commuting zones.
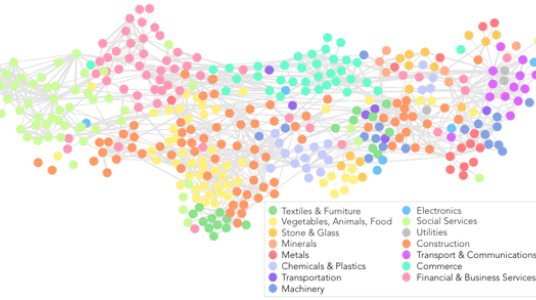
You can explore diversification opportunities for cities and states in Colombia using network mapping tools (as shown in the figure below) by visiting www.datlascolombia.com.
This research was conducted by Neave and colleagues primarily at the Center for International Development at Harvard University, in collaboration with Prof. Ricardo Hausmann, Eduardo Lora and Dr Andres Gomez. To see the working papers click the links:
The Path to Labour Formality: Urban Agglomeration and the Emergence of Complex Industry
City Size, Distance and Formal Employment Creation
Figure caption (click on it to enlarge): a network of labour flows between industries for Colombia. Nodes represent industries, and are colored by sector. It is observed that closely related industries tend to cluster, driven by workers transitioning between similar economic activities. This network models the flow of know-how within the Colombian economy, and can be used to model the path dependent process of industrial diversification for urban centres.