The concept of equilibrium is one of the most central ideas in economics. It is one of the core assumptions in the vast majority of economic models, including models used by policymakers on issues ranging from monetary policy to climate change, trade policy and the minimum wage. But is it a good assumption? In a paper just published in Science Advances, Oxford Mathematicians Marco Pangallo, Torsten Heinrich and Doyne Farmer investigate this question in the simple framework of games, and show that when the game gets complicated this assumption is problematic. If these results carry over from games to economics, this raises deep questions about economics models, and when they are useful for understanding the real world.
To understand what equilibrium is, it helps to think about a simple example. Kids love to play tic-tac-toe (also known as noughts and crosses), but at around eight years old they learn that there is a strategy for the second player that always results in a draw. This strategy is what is called an equilibrium in economics. If all the players in the game are rational they will play an equilibrium strategy. In economics, the word rational means that the player can evaluate every possible move and explore its consequences to their endpoint and choose the best move. Once kids are old enough to discover the equilibrium of tic-tac-toe they quit playing because the same thing always happens and the game is really boring. One way to view this is that, for the purposes of understanding how children play tic-tac-toe, rationality is a good behavioural model for eight year olds but not for six year olds.
In a more complicated game like chess, rationality is never a good behavioural model. The problem is that chess is a much harder game, hard enough that no one can analyse all the possibilities, and the usefulness of the concept of equilibrium breaks down. In chess no one is smart enough to discover the equilibrium, and so the game never gets boring. This illustrates that whether or not rationality is a sensible model of the behaviour of real people depends on the problem they have to solve. If the problem is simple, it is a good behavioural model, but if the problem is hard, it may break down.
Theories in economics nearly universally assume equilibrium from the outset. But is this always a reasonable thing to do? To get insight into this question, Pangallo and collaborators study when equilibrium is a good assumption in games. They don’t just study games like noughts and crosses or chess, but rather they study all possible games of a certain type (called normal form games). They literally make up games at random and have two simulated players play them to see what happens. The simulated players use strategies that do a good job of describing what real people do in psychology experiments. These strategies are simple rules of thumb, like doing what has worked well in the past or picking the move that is most likely to beat the opponent’s recent moves.
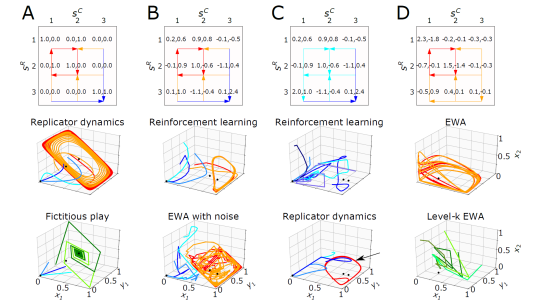
The authors find that the prevalence of cycles in the structure of games is a very good indicator of the likelihood that strategies do not converge to equilibrium. This point is illustrated in the figure below. Cycles are indicated with red arrows in the payoff matrices – namely, the tables filled with numbers in the first row. When cycles are present, many learning dynamics are likely to perpetually fluctuate instead of converging to equilibrium. Fluctuating dynamics are colored red or orange in the panels of the second and third rows.
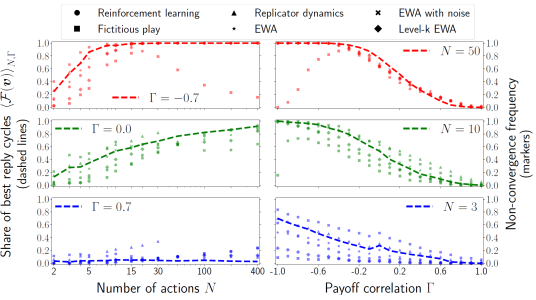
The theory then suggests that equilibrium is likely to be a wrong behavioral model when the game has a cyclical structure. When are cycles prevalent, and when are they rare?
When the game is simple enough, in the sense that the number of actions available to each player is small, cycles are rare. When the game is more complicated, whether or not cycles are common depends on whether or not the game is competitive. If the incentives of the players are lined up, cycles are rare, even if the game is complicated. But when the incentives of the players are not lined up and the game gets complicated, cycles are common.
These results match the intuition about noughts and crosses vs. chess: complicated games are harder to learn and it is harder for players to coordinate on an equilibrium when one player’s gain is the other player’s loss. The main novelty of the paper is that the authors develop a formalism to make all this quantitative. This is confirmed in the figure below, which shows the share of cycles (dashed lines) and the non-convergence frequency of six learning algorithms (markers) as the complicatedness and competitiveness of a game vary. (The payoff correlation Γ is negative when the game is competitive.)
Many of the problems encountered by economic actors are too complicated to model easily using a normal form game. Nonetheless, this work suggests a potentially serious problem. Many situations in economics are complicated and competitive. This raises the possibility that many important theories in economics may be wrong: If the key behavioural assumption of equilibrium is wrong, then the predictions of the model are likely wrong too. In this case new approaches are required that explicitly simulate the behaviour of the players and take into account the fact that real people are not good at solving complicated problems.