Graphs & Transformations
Part of the Oxford MAT Livestream
MAT syllabus
The graphs of quadratics and cubics. Graphs of
\begin{equation*}
\sin x, \quad \cos x, \quad \tan x, \quad \sqrt{x}, \quad a^x ,\quad \log_a x.
\end{equation*}
Solving equations and inequalities with graphs.
The relations between the graphs
\begin{equation*}
y = f (ax),\quad y = af (x),\quad y = f (x - a), \quad y = f (x) + a
\end{equation*}
and the graph of $y = f (x)$.
Revision
- The graph of an equation involving $x$ and $y$ is all the points in the $(x,y)$ plane that satisfy the equation. For a function $f(x)$, the graph of $y=f(x)$ shows the value of $f$ at each value of $x$.
- Quadratics $y=ax^2+bx+c$ have graphs like these
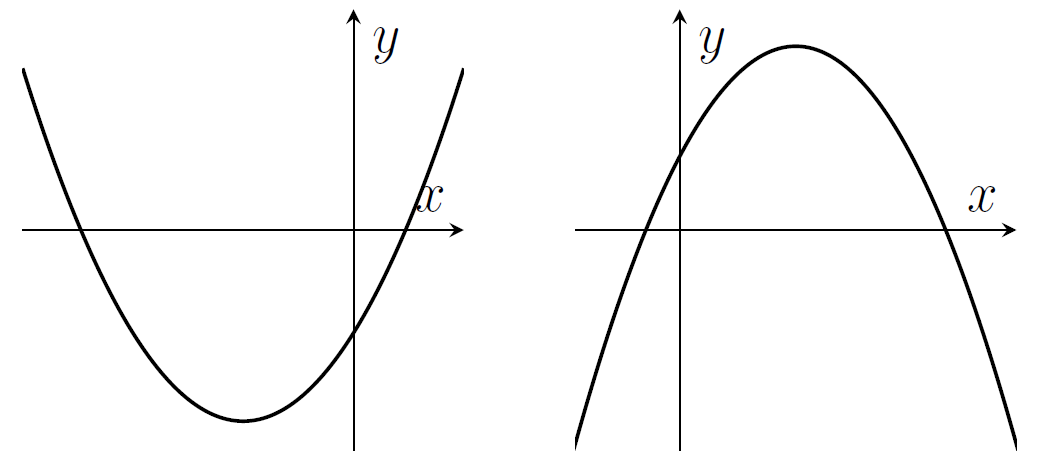
- Cubics $y=ax^3+bx^2+cx+d$ can have 0 or 1 or 2 turning points.
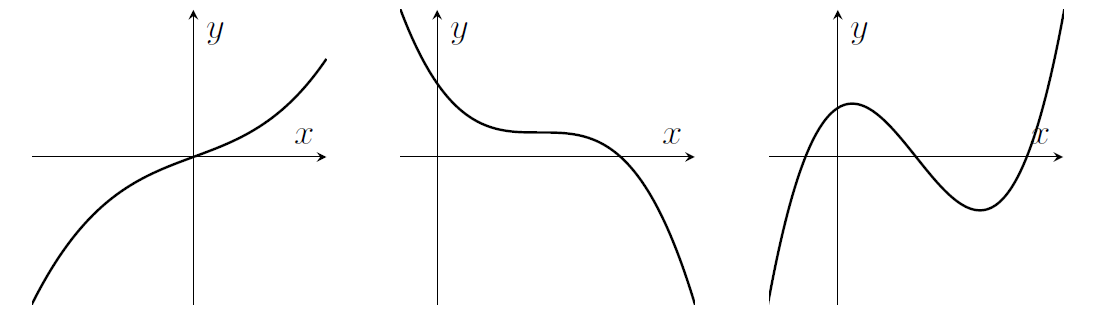
- Other polynomials have graphs that might have more turning points (up to $(n-1)$ turning points if $x^n$ is the highest power of $x$ in the polynomial)
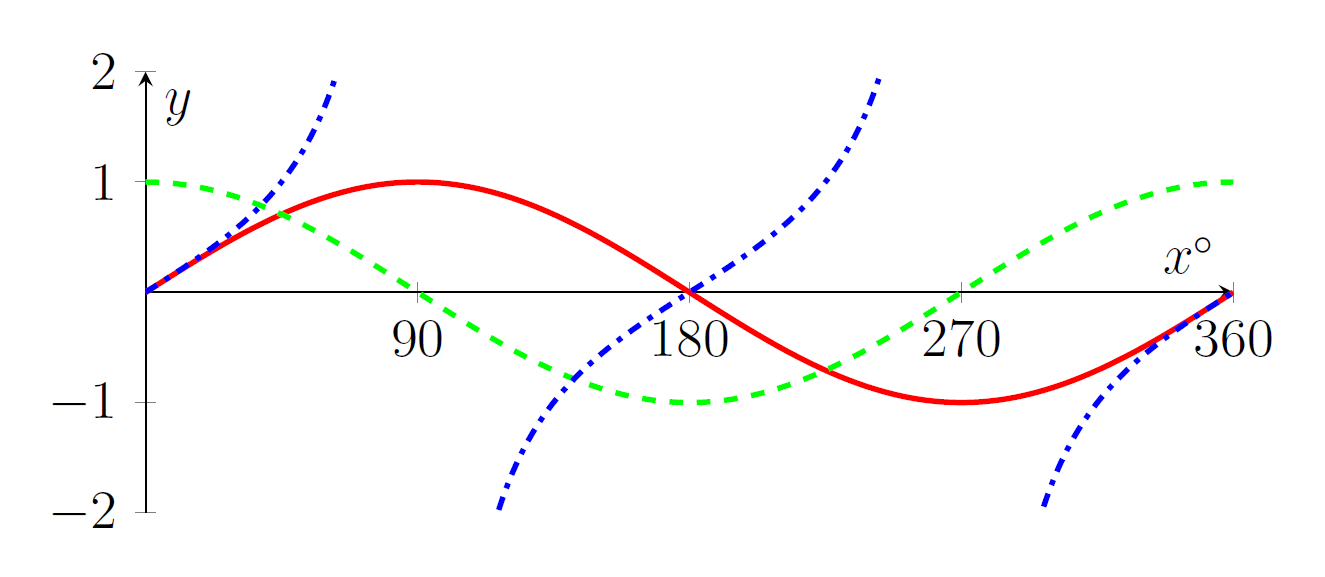
- Graphs of $y=\sin x$ (red solid line) and $y=\cos x$ (green dashed line) and $y=\tan x$ (blue dot-dashed line);
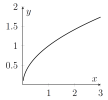
- Here are some more graphs. Note that $\sqrt{x}=x^{1/2}$ so the derivative is $\frac{1}{2}x^{-1/2}$, which gets arbitrarily large near $x=0$.
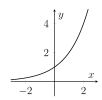
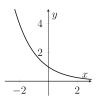
| $y=\sqrt{x}$ | $y=a^x$ with $a>1$ | $y=a^x$ with $0<a<1$ |
 |
 |
 |
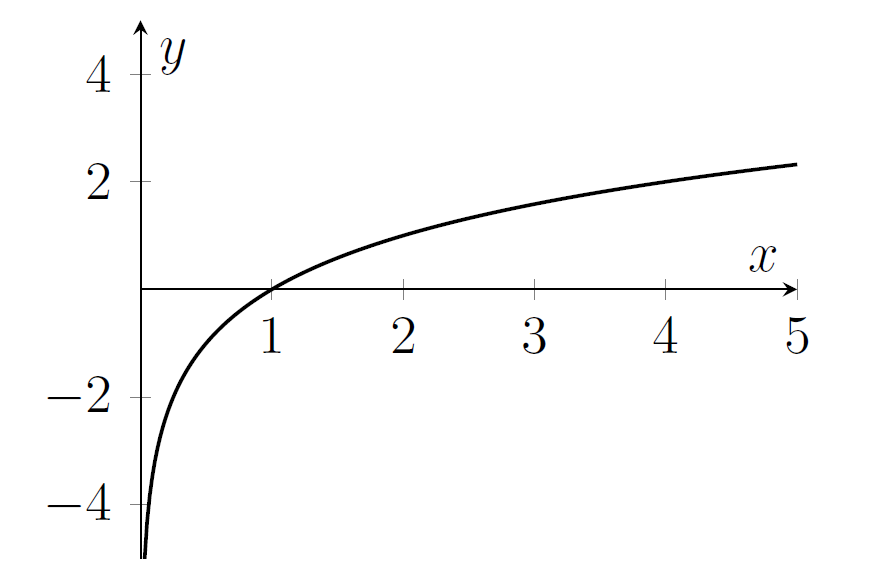
- Here's the graph of $\log_a x$. Note that $\log_a x$ is very negative for $x$ close to zero.
- The graph of $y=f(x-a)$ is the translation of the graph of $y=f(x)$ by a distance $a$ in the positive $x$-direction.
- The graph of $y=f(x)+a$ is the translation of the graph of $y=f(x)$ by a distance $a$ in the positive $y$-direction.
- The graph of $y=f(ax)$ is a stretch of the graph of $y=f(x)$ by a factor of $\frac{1}{a}$ parallel to the $x$-axis.
- The graph of $y=af(x)$ is a stretch of the graph of $y=f(x)$ by a factor of $a$ parallel to the $y$-axis.
Warm-up
- Sketch $y=ax^2+bx+c$ in each of the following eight cases;
- $a>0$, $b>0$, $c>0$
- $a>0$, $b>0$, $c<0$
- $a>0$, $b<0$, $c>0$
- $a>0$, $b<0$, $c<0$
- $a<0$, $b>0$, $c>0$
- $a<0$, $b>0$, $c<0$
- $a<0$, $b<0$, $c>0$
- $a<0$, $b<0$, $c<0$
In each case, decide how many roots there might be (there might be more than one possibility for the number of roots in some cases).
- Let $f(x)=x^2+4x+3$. Sketch the graph of $y=f(x+2)$.
- Sketch the graph of $y=3 f( 2 x)$.
- Sketch the graph of $y=2 f( 3 x)$. Is that the same as the previous graph?
- Let $f(x)=x^3-x$. Sketch the graph of $y=2f(x+1)$.
- Sketch the graph of $y=2f(x)+1$. Is that the same as the previous graph?
- Sketch the graph of $y=\log_2 x$. Sketch the graph of $y=\log_2 (x^2)$.
- Sketch the graph of $y=2^x$. Sketch the graph of $y=\left(\frac{1}{3}\right)^{x}$.
- Sketch the graph of $y= x\sqrt{2}$. Does the graph go through the point $\displaystyle \left(\frac{p}{q},\frac{r}{s}\right)$ for any positive whole numbers $p$, $q$, $r$, $s$?
- Sketch the graph of $y=\cos 2x$. Sketch the graph of $y=\frac{1}{2} + \frac{1}{2}\cos 2x$.
- Sketch all the points $(x,y)$ that satisfy $x+y=3$.
- Sketch all the points $(x,y)$ that satisfy $y^2=9x$.
- Sketch all the points $(x,y)$ that satisfy $x^2=4-y^2$.
MAT questions
MAT 2015 Q1I
Into how many regions is the plane divided when the following equations are graphed, not considering the axes?
\begin{eqnarray*}
y = x^3\\
y = x^4\\
y = x^5
\end{eqnarray*}
(a) 6,
(b) 7,
(c) 8,
(d) 9,
(e) 10.
Hint: Find any points of intersection. You might find that there are one or two points that lie on all three graphs. Don't forget to count any unbounded regions.
MAT 2014 Q1B
The graph of the function $y=\log_{10}\left(x^2-2x+2\right)$ is sketched in
(a) 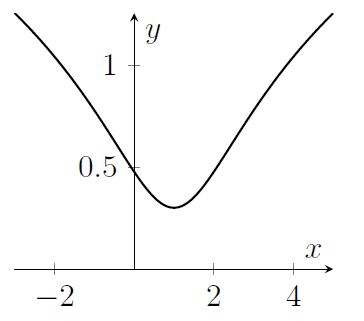
(b) 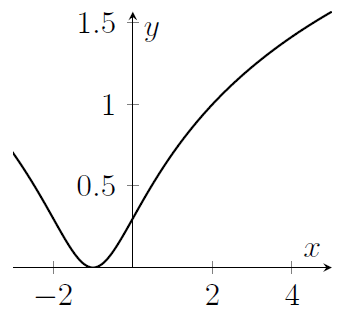
(c) 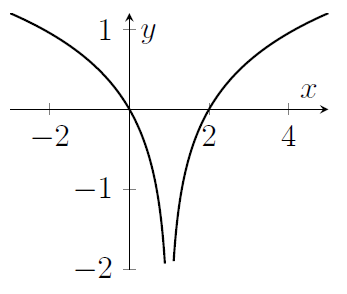
(d) 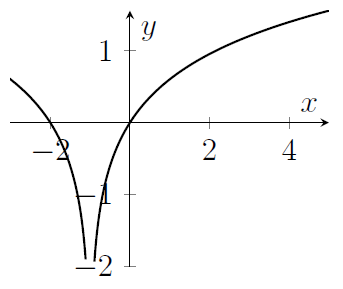
(e) 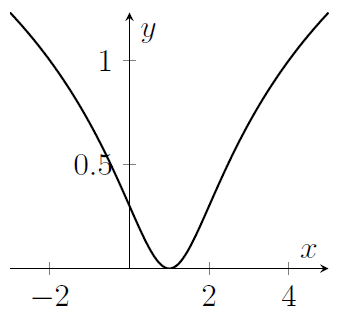
Hint: It would be good to know if the function inside the logarithm is ever zero.
MAT 2017 Q1D
The diagram below shows the graph of $y = f(x)$.
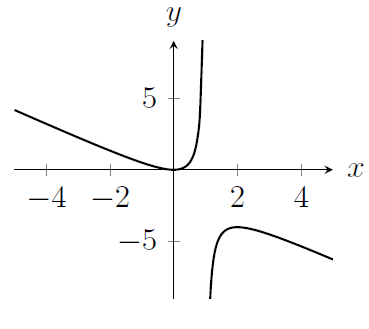
The graph of the function $y = -f(-x)$ is drawn in which of the following diagrams?
(a) 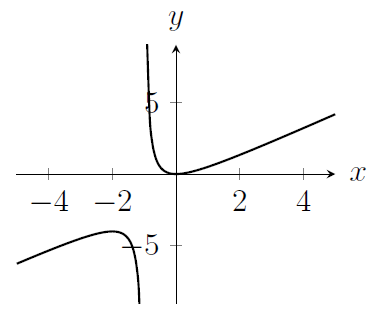
(b) 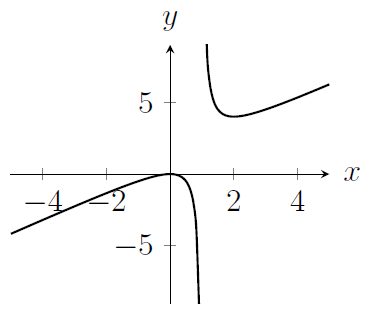
(c) 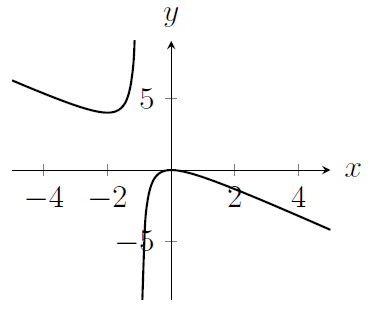
(d) 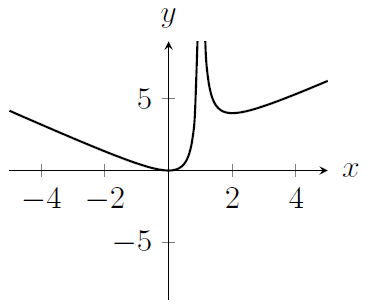
(e) 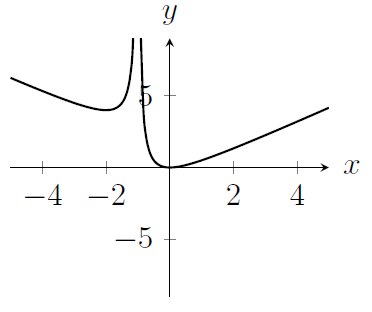
Hint: try to get to $-f(-x)$ in two steps, drawing pictures of what it looks like along the way.
MAT 2013 Q3
Let $0<k<2$. Below is sketched a graph of $y=f(x)$ where $f_k(x)=x(x-k)(x-2)$. Let $A(k)$ denote the area of the shaded region.
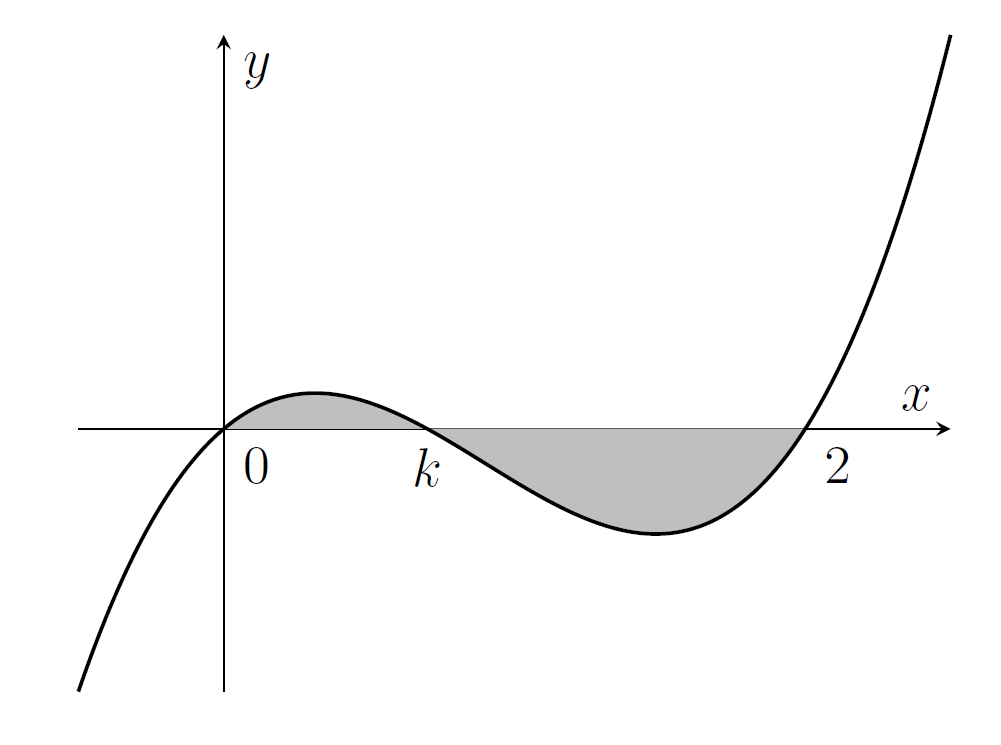
(i) Without evaluating them, write down an expression for $A(k)$ in terms of two integrals.
(ii) Explain why $A(k)$ is a polynomial in $k$ of degree 4 or less. You are not required to calculate $A(k)$ explicitly.
(iii) Verify that $f_k(1+t)=-f_{2-k}(1-t)$ for any $t$.
(iv) How can the graph of $y=f_k(x)$ be transformed to the graph of $y=f_{2-k}(x)$? Deduce that $A(k)=A(2-k)$.
(v) Explain why there are constants $a$, $b$, $c$ such that \[A(k)=a(k-1)^4+b(k-1)^2+c.\] You are not required to calculate $a$, $b$, $c$ explicitly.
Hints: The first two parts aren't about graphs or transformations, so you could skip them if you're not interested in practising integration right now. Quite often, the later parts of a MAT question are approachable even if you haven't done the previous parts.
In part (iii), note that we prove this with algebra (we know what $f_k(x)$ is, so just plug in the values). We'll need to be careful with the right-hand-side; $f_{2-k}(x)$ involves replacing each $k$ in the definition of $f_k$ with $(2-k)$. In general, it's important to know that you can sometimes use geometry or arguments about the symmetry of a graph, and sometimes you can just calculate away and do things like this with algebra.
In part (iv), you might need to apply more than one transformation; transform and then transform again!
Extension
The following material is included for your interest only, and not for MAT preparation.
There are lots of other interesting functions or equations that we might want to sketch. Here are some from the Oxford Online Maths Club, in no particular order and without context.
$$y=e^{-x}\cos x +\frac{1}{6}$$
$$y=e^{-x}\sin(x)$$
$$y=\sin(e^{-x})$$
$$y=\frac{x}{\ln x}\quad\text{and}\quad y=\frac{\ln x}{x}$$
$$y=\sin(x)-\sin(2x)\quad\text{and}\quad y=\frac{1}{2}\sin(x)-\frac{1}{16}\sin(2x)$$
$$y=x^3-\frac{35}{6}x^2+10x-\frac{25}{6}$$
$$y=\frac{1}{1+x^2}\quad\text{and}\quad y=\frac{1}{1+x^3}\quad\text{and}\quad y=\frac{1}{1+x^4}$$
$$y=\left(\frac{a}{x}\right)^{12}-\left(\frac{a}{x}\right)^6\quad \text{with $a>0$}$$
$$y=(\sin x)^2\quad\text{and}\quad y=(\sin x)^4\quad\text{and}\quad y=(\sin x)^6$$
$$y=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$
$$x^3+y^3=1$$
$$y=x^{1/2}\sin\left(\frac{1}{x}\right)$$
$$y=e^{-x}\left(x^2-4x+2\right)$$

