Envelopes of Geodesics on Ellipsoids
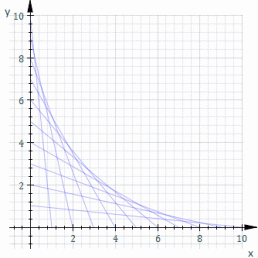
Given a family of curves, an "envelope" of the family is a curve which is at some point tangent to every curve in the family. An intuitive example of an envelope consists of a family of lines in $\mathbb{R}^2$, whose envelope is a parabola (click the animation below). If you move a point along a smooth curve, drawing the tangents, the envelope of this family of tangents is just the curve you started with.
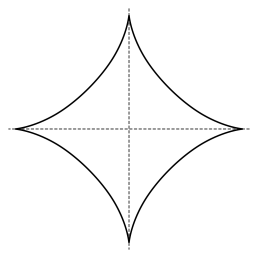
A nice example of envelopes is the astroid.This curve can be generated by sliding a line around so that its endpoints lie on the $x$ and $y$ axes with the $x$ coordinate of one end and the $y$ coordinate of the other adding up to 1 (click the circular image below for another neat construction of an astroid, as a hypocycloid). Note the first envelope is in fact a quarter of an astroid and for the complete curve you reat in the other three quadrants.
Envelope of Lines (© Sam Derbyshire), Astroid, Astroid Construction
Envelopes of Geodesics on Ellipsoids
Imagine two antipodal points on a sphere. All geodesics on a sphere are great circles, and all geodesics through a given point pass through its antipodal point. Three of our models (X 12a, 12b, 12c) illustrate how this changes for ellipsoids rather than spheres. The geodesics through a given point are now tangential to a 'squashed astroid'-shaped curve, centred about its antipodal point in the sense that the astroid's 'axes' meet there. Its 'axes' are in fact the lines of curvature through that point, drawn on each model. There is also an example geodesic line drawn through each chosen point, demonstrating the tangency property to the envelope. We see it meeting the envelope tangentially from two directions (recall that most geodesics on an ellipsoid are not closed). For more on envelopes of geodesics on ellipsoids, see here.
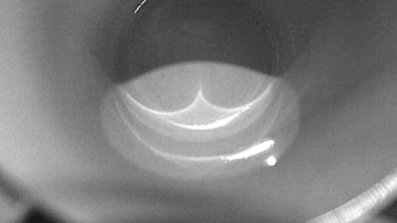
Thinking of the geodesics as 'light rays' in the surface, the squashed astroid is a caustic. Everyday-life occurences of caustics include nephroid caustics seen when a bright light shines onto a circular mug (the curve appears on the bottom), as well as the bright patches at the bottom of a swimming pool (both shown below). The link between physical optics (of waves) and geometric optics (of rays) is a famous example of perturbation methods (asymptotic analysis) in deriving the Eikonal equation from the wave equation. See here for more on caustics, and here for an interesting demonstration of the Eikonal equation as a model for the height of as pile of sand on a table.
Images: Caustic in a Mug (© Paul Venter); Underwater Caustic (© Brocken Inaglory)
Model X 12a is a tri-axial ellipsoid, with images of two envelopes shown below. They are each envelopes for points on the far side of the model, as described above.
Model X 12b is a spheroid, with images of two overlapping envelopes shown below. They are each envelopes for points on the far side of the model, as described above.
Model X 12c is another spheroid, with images of two overlapping envelopes shown below. They are each envelopes for points on the far side of the model, as described above.