Recursion
Part of the Oxford MAT Livestream
MAT syllabus
[There is no content on recursion explicitly on the MAT syllabus, but candidates are expected to be able to adapt their knowledge of sequences and series to more complex situations.]
Revision
See sequences and series.
- We might use the notation $a_{i,j}$ to refer to a sort of function that depends on two whole numbers $i$ and $j$, perhaps with some restrictions on the values that $i$ and $j$ can take, such as $0< j \leq i$. It might be convenient to imagine this as a table of values
| $i\downarrow$ \ $j\rightarrow$ | $1$ | $2$ | $3$ | $\dots$ |
| $1$ | $a_{1,1}$ | |||
| $2$ | $a_{2,1}$ | $a_{2,2}$ | ||
| $3$ | $a_{3,1}$ | $a_{3,2}$ | $a_{3,3}$ | |
| $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\ddots$ |
- We might write a function with two inputs as $f(x,y)$ or $f_y(x)$ or $f_x(y)$ depending on the context (but be consistent!)
Warm-up
- A sequence is defined by $a_0=3$ and then for $n\geq 1$ $a_n$ is the sum of all previous terms. Find $a_n$ in terms of $n$ for $n\geq 1$.
- The Fibonacci numbers are defined by $F_0=1$ and $F_1=1$ and then for $n\geq 2$, $F_{n}=F_{n-1}+F_{n-2}$. Find $F_{10}$.
- Suppose that we're trying to form a discussion group of $r$ people from a wider collection of $n$ people, one of whom is Sophie Germain. We'll write $f(n,r)$ for the number of different groups we can form. By considering separate cases for discussion groups that do or do not contain Sophie Germain, explain why \[f(n,r)=f(n-1,r)+f(n-1,r-1)\]
- A sequence is defined by $C_0=1$ and then for $n\geq 0$, $$\displaystyle C_{n+1}=\sum_{i=0}^{n}C_iC_{n-i}.$$
Find $C_1$ and $C_2$ and $C_3$ and $C_4$.
MAT questions
MAT 2014 Q5
Poets use rhyme schemes to describe which lines of a poem rhyme. Each line is denoted by a letter of the alphabet, with the same letter given to two lines that rhyme.
More precisely, the first line of the poem is given the letter A. If a subsequent line rhymes with an earlier line, it is given the same letter; otherwise, it is given the first unused letter. (For the purposes of this question, you can assume that we have an infinite supply of "letters'', not just the 26 letters of the alphabet.)
The purpose of this question is to investigate how many different rhyme schemes there are for poems of $n$ lines. We write $r_n$ for this number.
(i) There are five different rhyming schemes for poems of three lines (so $r_3 =5$). List them.
Let $c_{n,k}$ denote the number of rhyme schemes for poems of length $n$ that use exactly $k$ different symbols. For example $c_{3,2} = 3$ corresponding to the rhyming schemes AAB, ABA and ABB.
(ii) What is $c_{n,1}$ for $n \ge 1$? What is $c_{n,n}$? Explain your answers.
(iii) Suppose that $1<k<n$. By considering the final letter of a rhyming scheme, explain why
\begin{eqnarray*}
c_{n,k} = k c_{n-1,k} + c_{n-1,k-1}.
\end{eqnarray*}
(iv) Write down an equation showing how to calculate $r_n$ in terms of the $c_{n,k}$. Hence calculate $r_4$.
(v) Give a formula for $c_{n,2}$ in terms of $n$ (for $n \ge 2$). Justify your answer.
Hints: In part (iii) we're asked to explain why the equation works. We need to explain why the two terms give all the possible ways of making a rhyme scheme of length $n$ without double-counting or missing any. We should explain why there's a factor of $k$ in front of the $c_{n-1,k}$.
In part (v), we're looking for an explicit formula in terms of $n$, not in terms of other values of $c_{n,k}$, so we'll need to do some work to simplify things, justifying our work as we go. We might use the recurrence relation from part (iii), or we might choose to count the rhyme schemes directly.
MAT 2016 Q7
An $n$-fan consists of a row of $n$ points, the tips, in a straight line, together with another point, the hub, that is not on the line. The $n$ tips are joined to each other and to the hub with line segments. For example, the left-hand picture here shows a 6-fan,
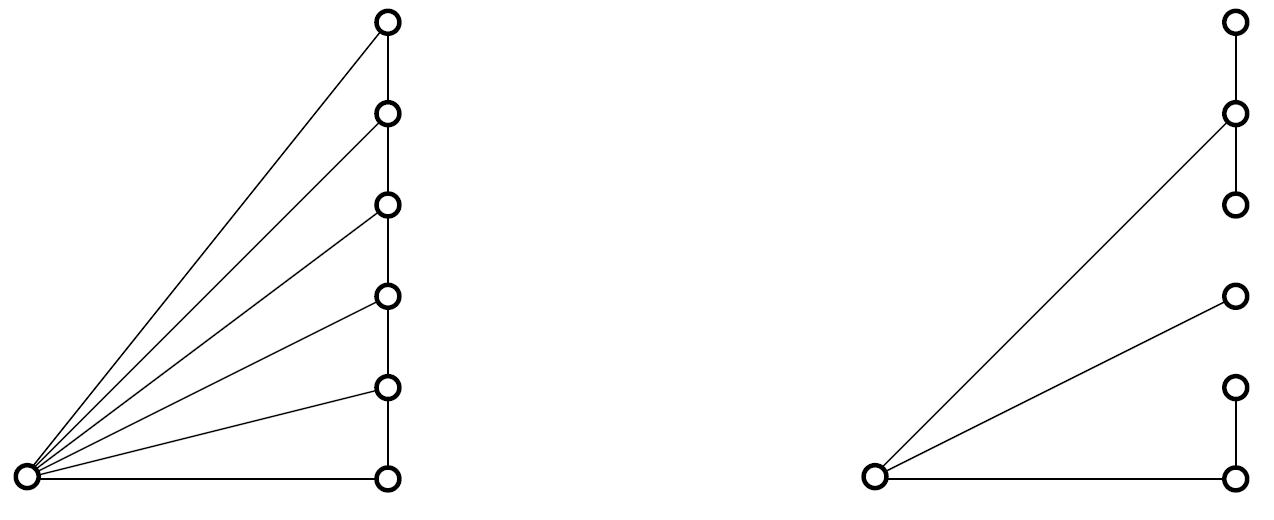
For a given $n$-fan, an $n$-span is a subset containing all $n+1$ points and $n$ of the line segments, chosen so that all the points are connected together, with a unique path between any two points. The right-hand picture shows one of many 6-spans obtained from the given 6-fan; in this 6-span, the tips are in groups of 3, 1 and 2, with the top group containing 3 tips.
(i) Draw all three 2-spans.
(ii) Draw all 3-spans.
(iii) By considering the possible sizes of the top group of tips and how the group is connected to the hub, calculate the number of 4-spans.
(iv) For $n\geq1$ let $z_n$ denote the number of $n$-spans. Give an expression for $z_n$ in terms of $z_k$, where $1\leq k<n$. Use this relationship to show that $z_5=55$.
(v) Use this relationship to calculate $z_6$.
Hints: In part (iii), the "top group" of tips in a 4-span are all connected to each other with vertical lines, and the next tip down is not connected to that group by a vertical line (so it must be connected to the hub via some other route).
In part (iv) we're asked to expand the reasoning in part (iii) from 4-spans to $n$-spans. The phrasing "in terms of $z_k$, where $1\leq k \leq n$" means that our expression can involve all previous values of $z_k$, possibly combined together in a complicated way!
Extension
A previous session of the Oxford MAT Livestream was on sequences and series, looking at more expressions that are like $a_n=f(a_{n-1})$.
The following material is included for your interest only, and not for MAT preparation.
The sequence $C_n$ in the warm-up is called the Catalan numbers. They're defined by $C_0=1$ and then for $n\geq 0$, $$\displaystyle C_{n+1}=\sum_{i=0}^{n}C_iC_{n-i}.$$
This sequence comes up in lots of different problems: here's one!
Consider splitting a regular $(n+2)$-sided polygon into $n$ triangles by connecting corners of the polygon (perhaps you're trying to demonstrate to someone that the sum of the internal angles of the polygon is $180^\circ n$). How many ways are there to do that?
Here's a heptagon that's been split into triangles as an example.
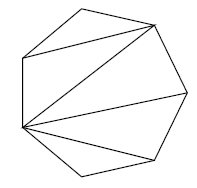
Look at the left edge of the heptagon. That edge must be part of a triangle (because the heptagon is split into triangles), and that triangle has corners at the endpoints of the edge. We can consider separate cases for where the other corner is (it must be one of the other five corners)

In the first case, we've got a left-over hexagon to split into triangles. In the second case, we've got a pentagon to split into triangles below the grey triangle, and a triangle above (only one way to split that into triangles!). Then in the third case we've got a quadrilateral above and a quadrilateral below. In each case, we can make choices about how to split up the space above the grey triangle independently of how we choose to split up the space below the grey triangle, so we should multiply the number of options together in each case.
If we write $a_n$ for the number of ways to split a regular $(n+2)$-sided polygon into $n$ triangles, then we have;
\[
a_5=a_4+a_1a_3+a_2a_2+a_3a_1+a_4
\]
If we define $a_0$ to be 1, then this is exactly the relationship that defines the Catalan numbers above. So the answer is that the number of ways to split a regular $(n+2)$-sided polygon into $n$ triangles is $C_{n}$.

