Multilevel Monte Carlo for Uncertainty Quantification in Brain Simulations

- Researcher: Matteo Croci
- Academic Supervisors: Patrick Farrell and Mike Giles
- Industrial Supervisor: Marie Rognes
Background
The motivation for this project is the analysis of the symptoms and causes of brain diseases. More specifically, we study the anomalies in the fluid dynamics of the brain that are believed to be related to dementia (which includes Alzheimer’s) and hydrocephalus. The movement of fluids within the brain can be simulated with the use of mathematical models. However, many of the parameter values in these models are subject to uncertainty and measurement errors. Can we quantify this uncertainty and discern how much this affects our model predictions? Which physiological parameters do we need to measure more accurately to obtain sensible predictions and useful insights?
The models we use are the Biot and convection-reaction-diffusion equations with random field coefficients. We use finite element techniques to solve these models and multilevel (quasi) Monte Carlo methods to quantify the uncertainty.
Outcomes
Numerical methods
To account for the uncertainty in our model, we replace the parameters subject to errors with random variables or Gaussian stochastic fields (random functions whose value at any point is given by a Gaussian random variable). Monte Carlo methods require the sampling of these parameters from their probability distributions. However, sampling Gaussian fields is non-trivial and computationally expensive.
The sampling problem can be recast as the solution of a partial differential equation with a random forcing term called white noise. White noise is a very rough and non-smooth object (see Figure 1). The lack of smoothness of white noise makes theoretical analysis of the finite element method (FEM) we are using to solve this equation complicated. In addition, when continuous Lagrange finite elements are used to solve the white noise equation, the sampling of white noise becomes expensive and approximations are generally used in practice. Despite these difficulties, we have shown that the FEM converges with optimal order and we presented a new white noise sampling technique that is cheap and efficient [1]. It works for any family of finite elements and is compatible with the multilevel Monte Carlo method. Once the white noise equation can be solved, Gaussian fields of arbitrary smoothness can be sampled (see Figure 1). The sampling method can be extended to the multilevel quasi Monte Carlo case (paper in preparation).
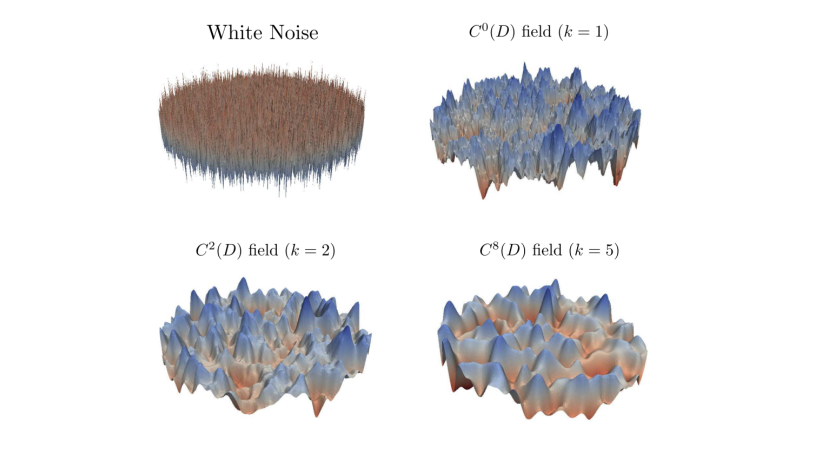
Figure 1: Realisations of different random fields. Top-left is highly non-smooth white noise, the rest are Gaussian fields of increasing smoothness.
Uncertainty quantification in mouse brain simulations
We applied the techniques described above to quantify the uncertainty in the Biot model when used to simulate the fluid movement in a mouse brain slice (see Figure 2). We were able to compute approximate high confidence intervals for various quantities of interest (e.g. the maximum interstitial fluid flux over time in a specific region). These quantities are important as there is active medical research trying to determine whether anomalies in these values are indicators of specific brain diseases.
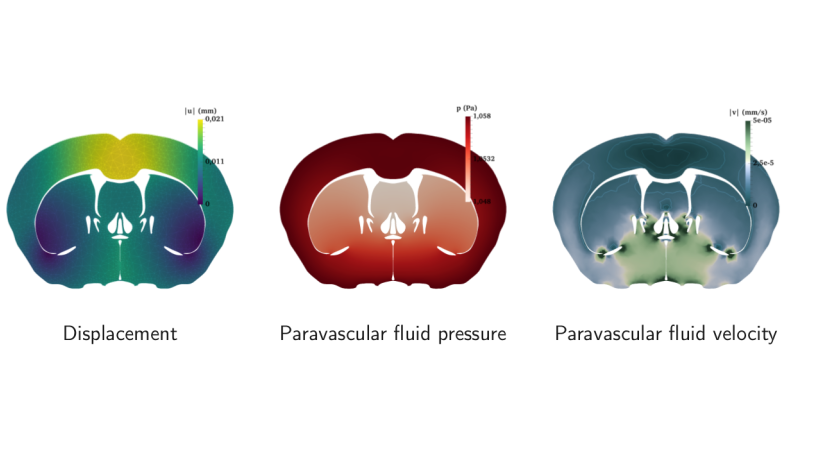
Figure 2: Expected behaviour of the mouse brain fluid dynamics. From left to right: expected displacement of the brain matter, expected paravascular fluid pressure and velocity.
Uncertainty quantification of tracer distribution in the human brain
In the final part of our research, we applied the above techniques and multilevel Monte Carlo simulations on real-life geometries to quantify the relative importance of diffusion
versus convection in the human brain under uncertainty in the physiological parameters, hence putting to test the glymphatic theory that states that solutes are cleared from the brain mainly by
convective transport. To do so, we constructed a new stochastic model describing the movement of a tracer (Gadobutrol) within the brain parenchyma. The outcome of our investigation supports the claim
that diffusion alone is not sufficient to explain transport of tracer as seen in MRI-images of studies in humans [3]. A paper describing the computational techniques used for the study is in preparation.

Figure 3. Tracer evolution in the human brain. Parenchymal tracer concentration after (from left to right) 1, 3, 8 and 24 hours of diffusion in (from top to bottom) sagittal, transverse and coronal planes. Initially, most of the tracer is found in inferior regions. At 24 hours, tracer has penetrated substantially into the gray matter, but not into the deep, central regions.
Publications
[1] M. Croci, M. B. Giles, M. E. Rognes, and P. E. Farrell. Efficient white noise sampling and coupling for multilevel Monte Carlo with non-nested meshes. SIAM/ASA Journal on Uncertainty Quantification, 6(4):1630–1655, 2018. doi: 10.1137/18M1175239.
[2] P. E. Farrell, M. Croci, and T. M. Surowiec. Deflation for semismooth equations. Optimization Methods and Software, pages 1–24, may 2019. doi: 10.1080/10556788.2019.1613655.
[3] M. Croci, V. Vinje, and M. E. Rognes. Uncertainty quantification of parenchymal tracer distribution using random diffusion and convective velocity fields. bioRxiv, jun 2019. doi: 10.1101/665109.

