Mathematics is delving in to ever-wider aspects of the physical world. Here Oxford Mathematician Alain Goriely describes how mathematicians and engineers are working with medics to better understand the workings of the human brain and in particular the issue of abnormal skull growth.
"In 2013, together with Prof. Antoine Jérusalem from the Engineering Department, I opened the International Brain Mechanics and Trauma Lab (IBMTL) here in Oxford. IBMTL is a network of people interested in the many and varied problems of brain mechanics and morphogenesis. As part of our launch, in true Oxford style, we organised a workshop where I got talking to Jayaratnam Jayamohan, aka Jay Jay, MD at the John Radcliffe Hospital in Oxford and a brilliant paediatric neurosurgeon whose work has featured in BBC documentaries. Jay Jay routinely performs surgery on children to rectify abnormal skull growth (so-called “craniosynostosis”).The variety of shapes and intricacy of growth processes that he talked about immediately captured my imagination. He explained that much has been learnt about this process from a genetic and biochemical perspective and the world expert, Prof. Andrew O. M. Wilkie, also happened to be working in Oxford. I decided to pay him a visit.
Andrew Wilkie has done groundbreaking work in identifying genetic mutations behind rare craniofacial malformations and, in my discussions with him, he was particularly helpful in explaining the mechanisms underlying this fascinating process. Yet, surprisingly, I found that very little was known about the physics and bio-mechanics of the problem. And when I was told that the problem of understanding the formation of these shapes was probably too complex to be studied using mathematical modelling tools, I realised I had a challenge I couldn’t possibly resist. What’s more I had the perfect partner in Prof. Ellen Kuhl at Stanford University. Ellen is an expert in biomechanical modelling and has developed state-of-the-art computational techniques to simulate the growth of biological tissues. We had much to work on.
The growth of the skull in harmony with the brain is an extremely complex morphogenetic process. As the brain grows, the skull must grow in response to accommodate extra volume while providing a tight fit. These are very different growth processes. The extremely soft brain increases in volume while the extremely hard bone must increase in surface area. How does this process take place?
In the spirit of mathematical modelling, we started with a very simple question: how would a given shape remain invariant during such growth processes? We know that the skull grows through two different processes: first, accretion along the suture lines (transforming soft cartilage into bone) and second, remodelling of the shape to change locally the curvature. Without remodelling, the shape cannot remain invariant (since surface addition mostly happens along a line, a point with initial high curvature away from this line would remain highly curved unless a second process enabled the reduction of the curvature so that the shape remains a dilation of the original shape).
Using dimensional arguments, we concluded that the three processes (volume growth, line growth, and remodelling) are inter-dependent and must necessarily be tightly regulated. But how is this process synchronized? Since the information about the shape is global, the cues that trigger the growth process must be physical as has been suggested in the biological literature. By simple physical estimates of pressure, stresses and strains, our analysis further identified strain as the main biophysical regulator of this growth process.
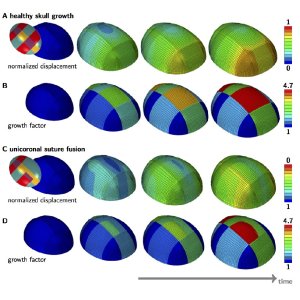
At this point, a natural question to ask is what happens when this process is disrupted? We decided to extract the fundamental elements of this growth process by looking at the evolution of a semi-ellipsoid (an elongated half-sphere) divided into a number of patches representing the various bones, fontanelles (soft spots), and sutures of the cranial vault. Normal growth process is obtained by allowing the bones to grow along the suture lines. However, we decided to perturb the system by fusing some of the suture lines early as happens during craniosynostosis. To our great surprise, the various shapes obtained mirrored the ones found in craniosynostosis. We showed that idealised geometries produce good agreement between numerically predicted and clinically observed cephalic indices (defined as the cranial vault’s width by its length) as well as excellent qualitative consistency in skull shape – in other words the model worked. The particular geometric role in the relative arrangement of the early cranial vault bones and the sutures appear clearly in our models. What is truly remarkable is that, despite the extreme complexity of the underlying system, the shapes developed in these pathologies seem to be dictated mostly by geometry and mechanics.
What's next? Our models are, of course, extremely simple from a biological standpoint. However, they can be easily coupled to biochemical processes in order to analyse several open questions in morphogenesis and clinical practice such as the impact of different bone growth rates, the relative magnitude of mechanical and biochemical stimuli during normal skull growth, and the optimal dimensions of surgically re-opened sutures. Our mechanics-based model is also a tool to explore fundamental questions in developmental biology associated with the universality and optimality of cranial design in the evolution of mammalian skulls. These questions were raised exactly a century ago by d’Arcy Thompson in his seminal book “On Growth and Form” and we now have the mathematical and computational tools to answer them. We are only at the beginning."
A fuller discussion of the issues can be found in Alain and his colleagues' recently published paper.