When compressed along its longest dimension, a thin structure such as a playing card collapses into a bent shape that accommodates the imposed compression without a significant change of length. This phenomenon of buckling under compression is ubiquitous in structural mechanics: bridges, marine vessels, and aerospace structures all risk failure due to buckling. Buckling is also widespread in nature: microtubules buckle within the cytoplasm and plant stems bend under their own weight.
Cycling is a sport where victory often hinges on marginal gains. In elite races like the Tour de France, while power output and aerodynamics are well-known performance factors another crucial, but less visible, element is risk. A crash, even if minor, can end a rider’s race. Can mathematics help optimise racing strategies in a world where both energy and safety must be balanced?
A new study uncovers a surprising connection between sliding droplets and migrating groups of cells. By combining live 3D imaging with mathematical modelling, scientists have revealed how cell collectives organise themselves in space and time, which depends on the cell collectives behaving like fluids.
Why do some memories last a lifetime while others fade away? A groundbreaking new study sheds light on this mystery by uncovering hidden patterns of brain activity that support long-term memory. Using a framework inspired by thermodynamics, scientists have developed a novel approach to understanding how different brain regions work together to shape cognition.
In this case study we survey the historical development of $\mathrm{Lip}(\gamma)$ functions, beginning with the work of Hassler Whitney from the 1930s and ending with some of the recent properties established by Terry Lyons and Andrew McLeod that are particul
A team of Oxford Mathematicians together with colleagues from the Oxford Botanic Garden and the University of Manchester has solved a mystery that has intrigued scientists for centuries. The squirting cucumber (Ecballium elaterium, from the Greek ‘ekballein,’ meaning to throw out) is named for the ballistic method the species uses to disperse its seeds. But how does it do it?
In a new study, Oxford Mathematician Coralia Cartis and Samar Khatiwala from Oxford's Department of Earth Sciences, together with colleagues and support from across the UK, Europe and the USA, have developed a novel approach to speed up the optimisation of ocean biogeochemical models - critical tools for predicting the impacts of climate change on marine ecosystems and the global carbon cycle.
Symmetry has been a guiding principle for physics ever since its modern conception in the work of Issac Newton, which eventually led to the reformulation of classical mechanics by Lagrange and Hamilton.
Mathematics and the natural world don't always see eye to eye; or rather shape to shape. When mathematicians study how tiles fit together, they keep it simple. Triangles, squares, and hexagons along with cubes and other polyhedra are built with sharp corners and flat faces. That works for maths.
But it doesn't work for Nature.
My recent research has been focused on the "sum-product phenomenon" which is a vast collection of results analysing the incongruence between additive and multiplicative structure over finite sets of numbers.
Filtration is a prevalent industrial process that may prove crucial in addressing some of the most important public health and environmental challenges of our time. In this case study, we discuss the need for more advanced filtration technology, and for academics to create user-friendly tools that meet that industrial need.
One of the most important questions in theoretical physics is finding a theory of quantum gravity, which could help us address fundamental questions about our world, related to what is inside a black hole, or what is the origin of the universe. Several approaches have been developed over the past decades to tackle this problem, with string theory being a leading candidate due to its potential to unify the laws of physics.
In this case study I report on a collaboration with Mo Dick Wong (Durham University), in the area of analytic and probabilistic number theory. We studied questions on a random model for the Möbius $\mu$ function. This function is one of the most elusive functions in number theory, and encodes deep questions on primes. Let's define it properly.
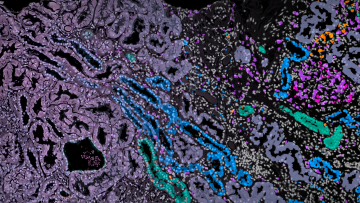
Globally kidney disease is forecast to be the 5th leading cause of death by 2040, and in the UK more than 3 million people are living with the most severe stages of chronic kidney disease. Chronic kidney disease is often due to autoimmune damage to the filtration units of the kidney, known as the glomeruli, which can occur in lupus, a disease which disproportionally affects women and people of non-white ethnicities, groups often underrepresented in research.
One of the greatest challenges in cancer treatment is maximising the response to a given drug - how can doctors get the greatest impact for the patient from the drug?
Traditionally, the answer to this has been ‘maximum tolerated dose’ (MTD) therapy, where the patient continually receives a high drug dose, with no breaks in treatment.
Systems of differential equations have a key role in biological and chemical models. These models come with parameters that show the model’s dependency on the environmental effects and often have unknown values. Model simulations from observation are desired not to be affected by the values of the parameters. In other words, we would like the parameters to be identifiable from the input-output behaviour of the system.
In mathematics, as in footwear, order matters. Putting on your socks before your shoes produces a different result to putting on your shoes before your socks. This means that the two operations 'putting on socks' and 'putting on shoes' are noncommutative. Noncommutative structures are widespread in mathematics, appearing in subjects ranging from group theory to analysis and differential equations.
We all know that mathematical activity goes on nowadays in a great variety of settings – not just in academia, but across the whole range of industry, education, and beyond. This diversity in mathematics is by no means new, and yet the study of the history of mathematics has often failed to capture it.