Research | Mathematical Institute - University of Oxford

Research

Departmental Research Centres and Groups

Algebra Research Group
Centre for Mathematical Biology
Combinatorics Group
Functional Analysis Group
Geometry Group - incorporating:
- Homological Mirror Symmetry
History of Mathematics Group
Mathematical Logic Group - incorporating:
- Analytic Topology
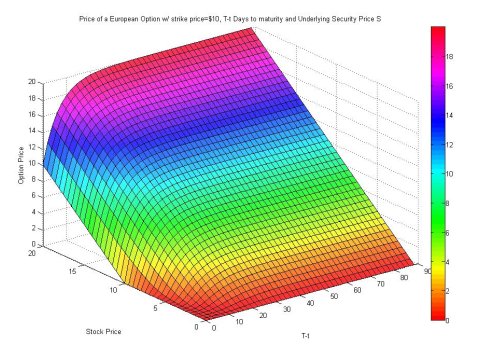
Mathematical and Computational Finance Group
Mathematical Physics Group - incorporating:
- Quantum Theory
- Relativity
Number Theory Group

Numerical Analysis Group
Oxford Centre for Collaborative Applied Mathematics
Oxford Centre for Industrial and Applied Mathematics - incorporating:
- Industrial Applications
- Mathematical Geoscience
- Differential Equations and Applications
- Fluid Mechanics and Materials
- Nonlinear Systems
- Applied Dynamical Systems and Inverse Problems
Oxford Centre for Nonlinear PDE
Stochastic Analysis Group
Topology Group

Other Research Networks, Collaborations etc

You may also be interested in research in the Department of Statistics and Computing Laboratory.

»

Printer-friendly version

Last updated by Keith A. Gillow on Tue, 17/11/2009 - 8:33am from a page originally created by Waldemar Schlackow.
This page is maintained by Chris Breward. Please use the contact form for feedback and comments.

All content (c) Copyright by Mathematical Institute | Accessibility Statement