Oxford Mathematician Ian Griffiths talks about his work with colleagues Galina Printsypar and Maria Bruna on modelling the most efficient filters for uses as diverse as blood purification and domestic vacuum cleaners.
"Filtration forms a vital part of our everyday lives, from the vacuum cleaners and air purifiers that we use to keep our homes clean to filters that are used in the pharmaceutical industry to remove viruses from liquids such as blood. If you’ve ever replaced the filter in your vacuum cleaner you will have seen that it is composed of a nonwoven medium – a fluffy material comprising many fibres laid down in a mat. These fibres trap dust particles as contaminated air passes through, protecting the motor from becoming damaged and clogged by the dust. A key question that we ask when designing these filters is, how does the arrangement of the fibres in the filter affect its ability to remove dust?
One way in which we could answer this question is to manufacture many different types of filters, with different fibre sizes and arrangements, and then test the performance of each filter. However, this is time consuming and expensive. Moreover, while we would be able to determine which filter is best out of those that we manufactured, we would not know if we could have made an even better one. By developing a mathematical model, we can quickly and easily assess the performance of any type of filter, and determine the optimal design for a specific filtration task, such as a vacuum cleaner or a virus filter.
As contaminants stick onto the surface of the filter fibres they will grow in size and we must capture this in our mathematical model to predict the filter performance. For a filter composed of periodically spaced and uniformly sized fibres, eventually all the fibres will become so loaded with contaminants that they will touch each other. At this point the filter blocks and we can terminate our simulation. However, for a filter with randomly arranged fibres, we may find ourselves in a scenario in which two fibres start off quite close to one another and so touch after trapping only a small amount of contaminant on their surface. At this point the majority of the rest of the filter is still able to trap contaminants and so we do not want to stop our filtration simulation yet. To compare the performance of filters with periodic and random fibre arrangements we therefore introduce an agglomeration algorithm. This provides a way for us to model two touching fibres as a single entity that also traps contaminants, and allows us to continue our simulation.
Filter devices operate in one of two regimes:
Case 1: the flow rate is held constant. This corresponds to vacuum cleaners or air purifiers, which process a specified amount of air per hour, but require more energy to do this as the filter becomes blocked.
Case 2: the pressure difference is held constant. This corresponds to biological and pharmaceutical processes such as virus filtration from blood. A signature of this operating regime is the drop observed in the rate of filtering fluid as the filter clogs up.
We divide our filters into three types, comprising: (i) uniformly sized periodically arranged fibres; (ii) uniformly sized randomly arranged fibres; or (iii) randomly sized and randomly arranged fibres. We compare the performance of each of these three filter types through four different metrics:
The permeability, or ease in which the contaminated fluid can pass through them.
The efficiency, or how much contaminant is trapped by the obstacles.
The dirt-holding capacity, or how much contaminant can be held in total before the filter blocks.
The lifetime, or how long the filter lasts.
Our studies show that:
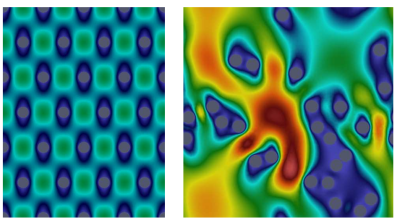
The permeability is higher for a filter composed of randomly arranged fibres than for a periodic filter. This is due to the ability for the contaminated fluid to find large spaces through which it can pass more easily (see figure below).
In Case 1, a filter composed of a random arrangement of uniformly sized fibres is shown to maintain the lowest pressure drop (i.e., require the least energy) with little compromise to the efficiency of removal and the dirt-holding capacity to that of a regular array of fibres.
In Case 2, a filter composed of randomly arranged fibres of different sizes gives the best removal efficiency and dirt-holding capacity. This comes at a cost of a reduced processing rate of purified fluid when compared with a regular array of fibres, but for examples such as virus filtration the most important objective is removal efficiency, and the processing rate is a secondary issue.
Thus, we find that the randomness in the fibres that we see in the filters in everyday processes can actually offer an advantage to the filtration performance. Since different filtration challenges will place different emphasis on the importance on the four performance metrics, our mathematical model can quickly and easily predict the optimum filter design for a given requirement."
Left: air flow through a filter composed of a periodic hexagonal array of fibres.
Right: air flow through a filter composed of a random array of fibres. In the random case a 'channel' forms through which the fluid can flow more easily, which increases the permeability.