Knot theory studies embeddings of the circle into the three dimensional space and the first knot invariant was the Alexander polynomial. The world of quantum invariants started with the milestone discovery of the Jones polynomial and was expanded by Reshetikhin and Turaev’s algebraic construction which starts from a quantum group and leads to link invariants. This method gives two important sequences of quantum invariants: coloured Jones polynomials $\{J_N(L,q) \}_{N \in \mathbb N}$ and coloured Alexander polynomials $\{\Phi_N(L, \lambda)\}_{N \in \mathbb N}$, which recover the original Jones and Alexander polynomials at the first terms.
Questions: Topological information encoded by quantum invariants
Up to this moment, the original Jones polynomial and Alexander polynomial have different natures. More precisely, the Alexander polynomial is well-understood in terms of the complement of the knot. However, the connection between the Jones polynomial and the topology of the knot complement is still a deep and mysterious question. Also, predictions from physics state that the limit of coloured Jones polynomials contain topological information of the complement such as the simplicial volume of the complement (Volume Conjecture).
Categorifications
A very powerful procedure called categorification starts with a polynomial invariant and aims to produce a sequence of groups which encode more information. Khovanov constructed a combinatorial categorification for the Jones polynomial and Ozsvath-Szabo and Rasmussen defined geometrical categorifications for the Alexander polynomial, called knot Floer homology. Later on, Seidel and Smith constructed a Floer type model for Khovanov's categorification. Dowlin showed recently that there is a spectral sequence between these two categorifications, but there are still questions about the geometry of such categorifications and spectral sequences.
On the homological side, Lawrence [5] introduced a sequence of representations $H_{n,m}$ of the braid group $B_n$ from the homology of a $\mathbb Z \oplus \mathbb Z$-covering of the configuration space of $m$ points in the $2n$-punctured disc. Related to this subject, Kohno [4], Ito and Martel worked on identifications between quantum and homological representations of braid groups. Based on Lawrence's work Bigelow [3] gave a topological model for the original Jones polynomial, as an intersection pairing between homology classes in coverings of configuration spaces. We call such a description a topological model.
Research program
I am working on a program aiming to obtain topological models for quantum invariants via intersections of Lagrangians in configuration spaces. This creates a new topological framework permitting one to read off topological information encoded by these invariants and having a goal of achieving geometrical categorifications.
Topological models for $U_q(sl(2))$-quantum invariants
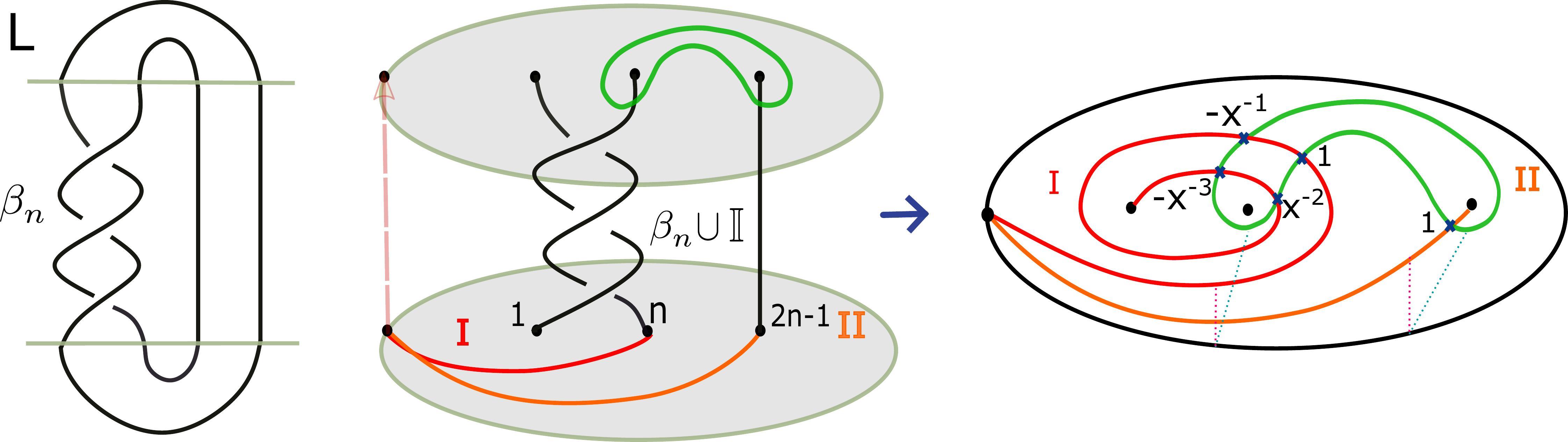
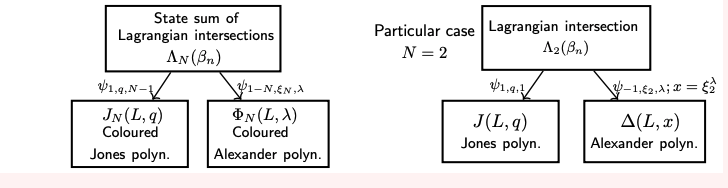
My main results [1], [2] show a unified topological model for the $N^{th}$ coloured Jones and $N^{th}$ coloured Alexander invariants. We define a state sum of graded intersections between Lagrangians in a configuration space in the punctured disk (over $3$ variables) recovering the $N^{th}$ coloured Jones and the $N^{th}$ coloured Alexander polynomial. We will use:
1) Lawrence representations $H_{n,m}$ and $H^{\partial}_{n,m}$ which are $\mathbb Z[x^{\pm 1},d^{\pm 1}]$-modules which carry a $B_n$-action
2) Intersection pairing $\langle , \rangle: H_{n,m} \otimes H^{\partial}_{n,m}\rightarrow \mathbb Z[x^{\pm},d^{\pm}]$ Poincaré-Lefschetz type duality
This pairing is encoded by the intersections in the base configuration space, graded by the local system.
Homology classes
The construction of the Lagrangians is done by drawing certain curves in the punctured disc, taking their product and quotienting it in the unordered configuration space. Using this, for any indices $i_1,...,i_{n-1} \in \{0,...,N-1\}$ we define two Lagrangians and consider two classes given by their lifts:
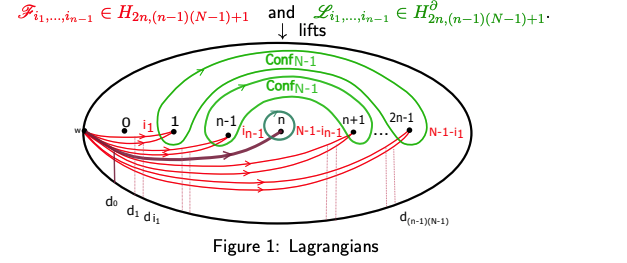Theorem (Unified model through a state sum of Lagrangian intersections [2]) Let $L$ be an oriented link and $\beta_n \in B_n$ such that $L=\hat{\beta}_n$ (as braid closure). We consider the following state sum of Lagrangian intersections $\Lambda_N(\beta_n)(u,x,d) \in \mathbb Z[u^{\pm1},x^{\pm 1},d^{\pm 1}]$: $$\Lambda_N(\beta_n)(u,x,d):=u^{-w(\beta_n)} u^{-(n-1)} \sum_{i_1,...,i_{n-1}=0}^{N-1} \langle(\beta_{n} \cup {\mathbb I}_{n} ){ \mathscr F_{i_1,...,i_{n-1}}}, { \mathscr L_{i_1,...,i_{n-1}}}\rangle.$$Then, $\Lambda_N$ recovers the $N^{th}$ coloured Jones and $N^{th}$ coloured Alexander invariants: \begin{equation} \begin{aligned} &J_N(L,q)=\Lambda_N(\beta_n)|_{\psi_{1,q,N-1}}\\ &\Phi_{N}(L,\lambda)=\Lambda_N(\beta_n)|_{\psi_{1-N,\xi_N,\lambda}}. \end{aligned} \end{equation} (here $w(\beta_n)$ is the writhe of the braid, $\psi_{c,q,\lambda}$ a specialisation of the coefficients and $\xi_N=e^{\frac{2\pi i}{2N}}$)
Corollary
We can read off the $N^{th}$ coloured Jones polynomial and the $N^{th}$ coloured Alexander polynomial from the same geometric picture, given by the graded intersection between the above Lagrangians, in the configuration space of $(n-1)(N-1)+1$ particles in the $2n$-punctured disk.
Figure 2: Jones and Alexander polynomials of the trefoil knot
Framework for categorifications of quantum invariants
This explicit model sets up a framework for investigating categorification problems for the whole families of coloured Alexander polynomials and coloured Jones polynomials. Moreover, it provides a tool for understanding possible relations between them.
We think that the state sum $\Lambda_2(\beta_n)$ (for the case $N=2$) leads to knot Floer homology of $L$ (specialised through $\psi_{-1,\xi_2,\lambda}$). We expect that a cousin of this state sum (obtained from immersed Lagrangians given by figure eights as in [2] $\Omega_2(\beta_n)$ leads to a geometrical categorification for the Jones polynomial. Moreover, we expect that these two results will lead to a spectral sequence between categorifications of the Jones polynomial and knot Floer homology.
Cristina Anghel is a Postdoctoral Research Associate in Oxford Mathematics. You can watch a short film introducing her work here.
References
[1] C. Anghel - Coloured Jones and Alexander polynomials as topological intersections of cycles in configuration spaces, math.GT arXiv:2002.09390, 47 pages, (2020).
[2] C. Anghel - $U_q(sl(2))$−quantum invariants unified via intersections of embedded Lagrangians, math.GT arxiv: 2010.05890, 24 pages, (2020).
[3] S. Bigelow - A homological definition of the Jones polynomial, Invariants of knots and 3-manifolds Kyoto, 2001, Geom. Topol. Monogr. 4, 29-41, (2002).
[4] T.Kohno - Monodromy representations of braid groups and Yang–Baxter equations, Ann. Inst. Fourier (Grenoble) 37, 139–160 (1987).
[5] R. J. Lawrence - A functorial approach to the one-variable Jones polynomial, J. Differential Geom., 37(3):689–710, (1993).