In quantum many body physics, we look for universal features that allow us to classify complex quantum systems. This classification leads to phase diagrams of quantum systems. These are analogous to the familiar phase diagram of water at different temperatures and pressures, with ice and vapour constituting two phases. Quantum phase diagrams correspond to the different phases of matter at zero temperature, where the system is in its lowest energy state (usually called the ground state).
Generic states of a quantum many body system are difficult to describe since all of the constituent parts are quantum entangled with one another. This means that, counterintuitively, we cannot view the state of the whole system as being built up of a state of each part separately; one must consider the system as a whole. An important theoretical result is that for one-dimensional systems (for example, quantum wires), the ground states (of 'gapped phases') obey an area law for entanglement [1]. This quantifies, in a way that can be made precise, the amount of entanglement. States of this form are sufficiently entangled to form exotic quantum phases of matter. Despite this, states obeying an area law have a relatively small amount of entanglement and so can be well-approximated by a simple family of states called matrix-product states (MPS). MPS have been widely studied over the last decades and are an important analytical and numerical tool [2]. Click here for technical aside: what is an MPS?
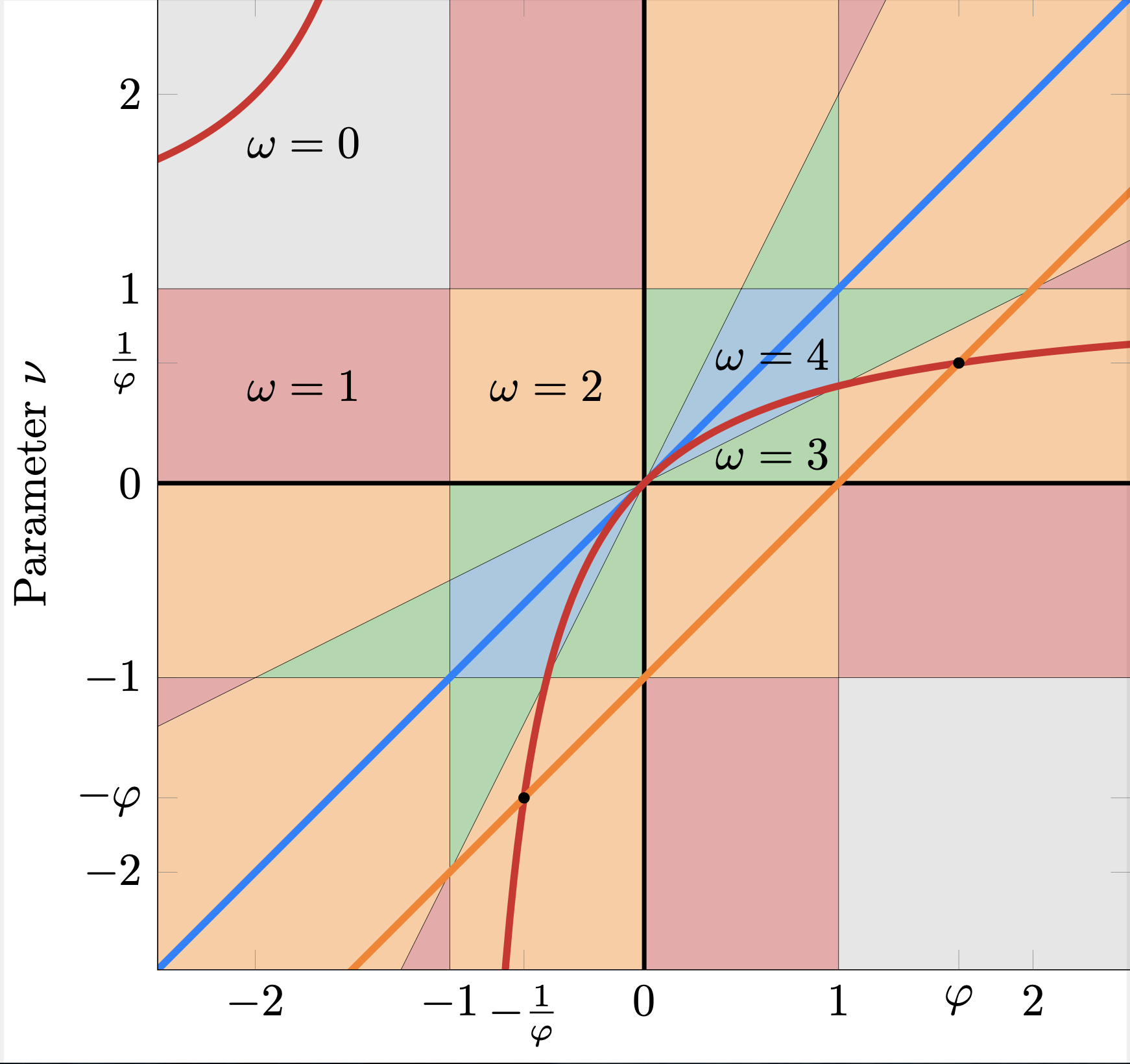
However, this is usually only an approximation (albeit, due to the area law, a good one) - the true ground state cannot usually be represented by an exact MPS. One can ask the question: which family of states within the phase diagram have ground states that can be exactly described by an MPS? In a recent work with Julian Bibo, Bernhard Jobst, Frank Pollmann, Adam Smith and Ruben Verresen, we called this family the MPS skeleton, as it is a basic structure supporting the rest of the phase diagram. Indeed, the skeleton connects the different phases of matter: the bones of the skeleton are paths through the phase diagram, corresponding to tuning physical coupling constants. Paths through distinct phases of quantum matter meet at critical points: these form joints of the skeleton. An example of an MPS skeleton is given in the following figure for a particular family of models, where the different colours correspond to different universality classes (labelled by different integers $\omega$).
The phase diagram of the BDI model described by the function $ f(z) = (z-\mu)(z-\nu)\left(z-\frac{\mu-\nu}{\mu}\right)\left(z-\frac{\mu-\nu}{\nu}\right)$; the differently shaded regions show the different phases labelled by integers $\omega$. The solid blue, red and orange lines show the MPS skeleton: parameterized paths along which we can find the MPS representation of the ground state. $\varphi=(1+\sqrt{5})/2$ is the golden ratio. (Figure from Ref. [3])
While the problem of identifying the MPS skeleton is rather general, we study it in tractable classes of free-fermion models. In [3] we give a complete characterization of this MPS skeleton for the BDI class of free spinless fermions with time-reversal symmetry, as well as a construction for the MPS as a function of physical tuning parameters (i.e., a method of constructing the tensor $A$). This is an important class: the different phases are labelled by an integer $\omega$, and a representative for each different phase is a stack of $\omega$ many 'Kitaev chains'. The Kitaev chain has interesting physics, in particular it has so-called Majorana edge modes at the ends of the chain (or wire). These modes are 'topologically protected' and are of interest, for example, in applications to quantum information processing in wire networks [4].
In the case of the BDI class, the mathematical characterisation of the MPS skeleton is quite neat. First, any model in this class can be specified by a set of physical coupling constants $\{t_\alpha\}$; these are real numbers. One can think of the number $t_\alpha$ as expressing the likelihood that a fermion on one site will hop to another site at a distance $\alpha$ away. With these coupling constants fixed, we can write a corresponding complex (Laurent) polynomial of the form: $$f(z) = \sum_{\alpha=p}^n t_\alpha z^\alpha =z^{p} \prod_{j=1}^{n-p}(z-z_j),$$ where $p$ can be positive or negative and $z_j$ are the zeros of the polynomial. If $f(z) = z^p g(z)^2$ then it has an MPS ground state. The construction of the MPS tensor depends in a simple way on the coefficients of the 'square-root' polynomial $g(z)$; from this we derive a circuit construction of the ground state leading to the MPS. The part of the skeleton where this can be written as a unitary circuit can be particularly efficiently processed on a noisy intermediate-scale quantum (NISQ) computer. Indeed, a special case of this construction, where $f(z) = (z-a)^2$, has been analysed previously [5] and was recently studied on a NISQ device [6].
In [7] we give a different perspective on the MPS skeleton, studying free-fermion models that satisfy $f(z) = z^p g(z)^2$ using Toeplitz determinant theory. Applying beautiful results of Day and Gorodetsky [8-11] leads us to remarkable exact formulae for certain physically important correlation functions as well as for the characteristic polynomial of the correlation matrix, itself intimately related to entanglement properties. These results again imply the existence of an MPS ground state for this subclass of models in the BDI class, although in this case the argument is not constructive (and so does not give us the tensor $A$). It does, however, easily extend to another class of free-fermion models (so-called class AIII), and hence we can identify the MPS skeleton in that case.
It is an exciting open question to identify the MPS skeleton in further classes of models.
NIck Jones is a Research Fellow in Oxford Mathematics.
References:
[1] An area law for one-dimensional quantum systems, M B Hastings; J. Stat. Mech. (2007) P08024
[2] Matrix Product States and Projected Entangled Pair States: Concepts, Symmetries, and Theorems, Ignacio Cirac, David Perez-Garcia, Norbert Schuch and Frank Verstraete; arXiv:2011.12127
[3] Skeleton of Matrix-Product-State-Solvable Models Connecting Topological Phases of Matter, Nick G. Jones, Julian Bibo, Bernhard Jobst, Frank Pollmann, Adam Smith, Ruben Verresen; Phys. Rev. Research 3, 033265 (2021)
[4] Non-Abelian statistics and topological quantum information processing in 1D wire networks, Jason Alicea, Yuval Oreg, Gil Refael, Felix von Oppen, and Matthew P. A. Fisher; Nature Physics 7, 412-417 (2011)
[5] Quantum phase transitions in matrix product systems, Michael M. Wolf, Gerardo Ortiz, Frank Verstraete and J. Ignacio Cirac; Phys. Rev. Lett. 97, 110403 (2006)
[6] Crossing a topological phase transition with a quantum computer, Adam Smith, Bernhard Jobst, Andrew G. Green and Frank Pollmann; arXiv:1910.05351
[7] Exact correlations in topological quantum chains, Nick G. Jones and Ruben Verresen; arXiv:2105.13359
[8] Toeplitz Matrices Generated by the Laurent Series Expansion of an Arbitrary Rational Function, K.M. Day; Transactions of the American Mathematical Society (1975) 224
[9] Toeplitz determinants generated by rational functions, M. Gorodetsky; in Integral and Differential Equations and Approximate Solutions, Dybin, ed., pp. 49–54, Elista (1985)
[10] Toeplitz determinants generated by rational functions, M. Gorodetsky; Deposited at Viniti 1981, RZhMat 1982: 3 A444.
[11] Status report on rationally generated block Toeplitz and Wiener-Hopf determinants, A. Böttcher; Unpublished manuscript (1989)
Technical aside: what is an MPS?
For a translation-invariant chain of $N$ sites, where each site has $d$ levels (e.g., a qubit corresponds to $d=2$), MPS are wavefunctions of the form: $$\lvert \psi \rangle = \sum_{j_1 \dots j_N =1}^d \mathrm{tr}(A^{j_1} \dots A^{j_N} )\lvert j_1 \dots j_N \rangle$$ where, for a fixed $j \in \{1,\dots,d\}$, $A^j$ is a $\chi \times \chi$ matrix for some fixed $\chi$. The parameter $\chi$ is called the bond-dimension and we are interested in cases where $\chi$ is independent of $N$. (If we allow $\chi$ to grow with system size then any state can be written in this form!) The state in an exponentially large Hilbert space (with dimension $d^N$) is specified by the $d\chi^2$ entries of the tensor $A$.