Towards the end of the eighteenth century, French mathematician and engineer Gaspard Monge considered a problem. If you have a lot of rubble, you would like to have a fort, and you do not like carrying rocks very far, how do you best rearrange your disorganised materials into organised walls? Over the two centuries since then, his work has been developed into the rich mathematical theory of optimal transport. Combined with recent advances in computational techniques, optimal transport has proven useful in contexts ranging from image classification to the pure mathematics of Alessio Figalli's Fields Medal. We now use it in biology, as a step in translating RNA sequencing measurements to useful biological knowledge.
Single-cell RNA sequencing offers an unprecedented window into cell biology, revealing how your body builds wildly different cell types, from skin cells to neurons, from the same underlying DNA. After sequencing, each cell is represented as a vector of gene expression, where each component is the count of RNA molecules observed in that cell corresponding to a particular gene. The key challenge is that standard experimental techniques destroy the measured cells and therefore cannot be used to follow the same cell over time. Learning time dependence, however, is critical for applications. We want to know, for example, what the future state of a tumour will be based on a biopsy of cancer cells. This is the problem of trajectory inference.
A substitute for measuring the same cell at multiple times is to prepare similar populations of cells and measure each after a different amount of time. Erwin Schrödinger showed that a regularised version of optimal transport provides the maximum likelihood coupling between an initial and final distribution of diffusing particles. This mathematically rigorous way of connecting a series of static snapshots of a dynamic process is now the core of Waddington-OT, a state of the art method for reconstructing trajectories from gene expression data.
Figure 1: The question of optimal transport: how do we convert one distribution of rocks to another without doing too much work?
Recent technologies augment the gene expression data with lineage barcodes, allowing inference of a lineage tree encoding the ancestral relationships among a population of sampled cells. Intuitively, knowing which cells are closely related to each other ought to give information about their historical states, but how? Some natural ideas for using lineage tracing to improve trajectory inference do not work. Directly matching the measured lineage trees across time points, for example, is complicated by sampling noise and biological variability.
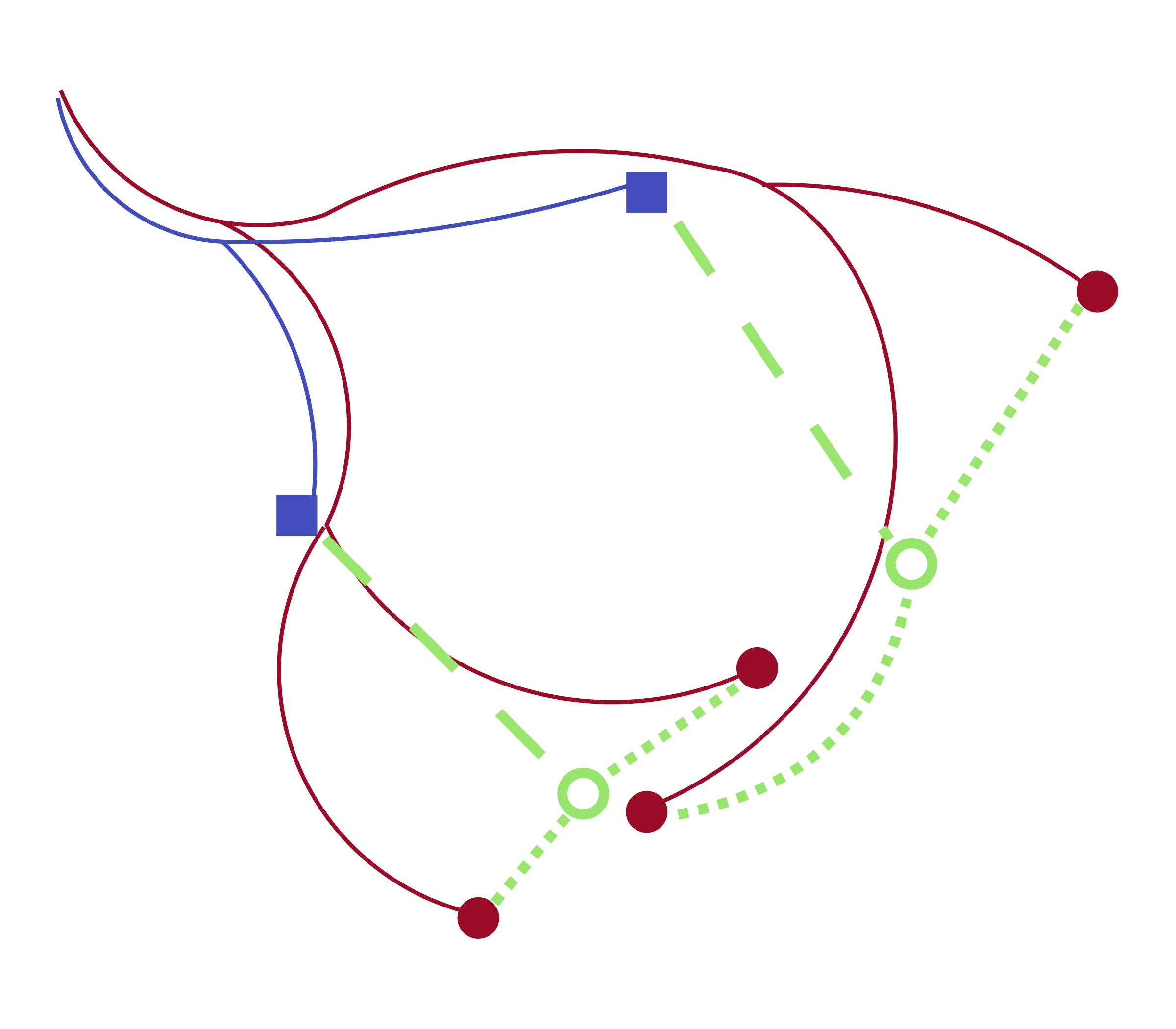
We developed a tool by returning to the mathematical justification for optimal transport. Following Schrödinger, an optimal transport coupling is a maximum likelihood estimate based on a model of independent diffusion. Given a lineage tree, however, the past trajectories of observed cells are not independent but correlated in a way that still allows efficient maximum likelihood estimation. This logic leads to a two-step process for fitting couplings: estimate initial guesses for the ancestral gene expression of cells measured at the late time point, then use optimal transport to couple to the early samples.
Figure 2: Our algorithm matches sampled cells at a later time point (red circles) to sampled cells at an earlier time point (blue squares) by first estimating ancestor locations (empty green circles) and then applying optimal transport.
Through a combination of simulated examples and tests on sequencing data from C. elegans, we demonstrated that adding lineage information in this way does indeed improve the accuracy of fitted trajectories, particularly in cases where cells converge to the same final state via different paths. This is one more step towards a comprehensive solution to the trajectory inference problem, which would have broad impacts across biology and medicine.
Aden Forrow is a Research Fellow in the Mathematical Institute in Oxford.