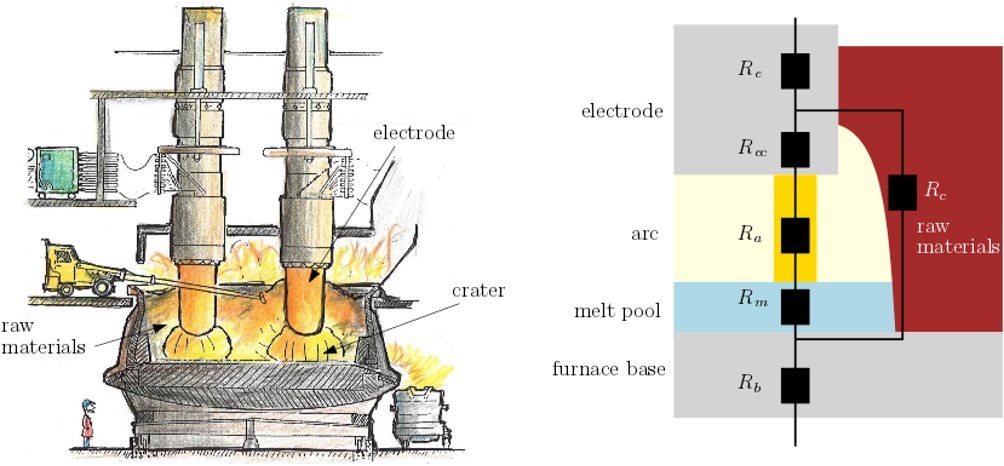
Silicon is produced industrially in a submerged arc furnace (illustrated in Figure 1, left), with the heat required for the endothermic chemical reaction provided by an electric current. The high temperatures within the furnace (up to around 2000 K) prohibit observation of the internal conditions, so that mathematical modelling is a valuable tool to understand the furnace processes.
The electric currents and voltages over the furnace are some of the few measurements that are taken during furnace operation, and from these readings furnace operators attempt to infer the internal state of the furnace. However it is not well understood what the changes in these electrical measurements mean physically, and how they relate to the efficiency of the silicon production.
Figure 1: Illustration of a silicon furnace, adapted from TH Hannesson; The Si Process Drawings (left), and a portion of the electric circuit diagram for the furnace, showing the resistive components (right).
One way to understand the electrical measurements is to compare them to mathematical models of the furnace system. The furnace may be modelled as an electric circuit, with the electrodes and raw materials viewed as components in the circuit, with known electrical resistances. One particularly difficult aspect of the electrical system is the electric arcs which carry the current through hot, gas-filled craters within the bed of material in the furnace. In these arc regions the gas is heated to around 20,000K and ionised to a plasma, so that the dissociated electrons and ions can carry the electrical current. The electromagnetic forces generate a high-velocity flow of the plasma, and since the ionisation of the plasma increases with temperature, the size and shape of the electrically-conductive region is determined by the interacting heat generation, convection, and losses. Within the electric-circuit furnace models, the arc resistances are generally assumed to depend on the oscillating voltage over the arc, and are given by empirical ODE models. However, these empirical models were designed for other applications, and do not capture all the features of furnace arcs.
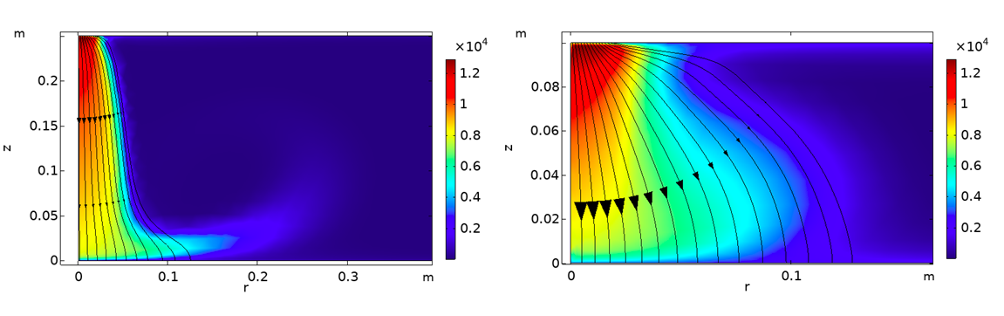
Figure 2: Axisymmetric simulations of a MHD model for an electric arc, showing the current density (streamlines) and the electrical conductivity (colour, units S/m) for a tall arc (left) and shorter arc (right).
We are studying a magnetohydrodynamic (MHD) model for electric arcs, which couples the Navier-Stokes equations for the fluid flow and Maxwell’s equations for the electromagnetic fields with an equation of conservation of energy in the arc fluid. Some simulations of this model are shown in Figure 2. A dimensional analysis of this MHD model suggests that, in the silicon furnace, the heat radiation is the dominant heat loss mechanism from the arc. We have proposed a simple model for the arc resistance, assuming that the resistive heating and the radiative heat loss are the only important heat transfer effects. Compared with the empirical models, our model captures the high-current behaviour of the arcs more accurately, predicting a quasi-steady, rising current-voltage characteristic in the high-current periods of the alternating current cycle. Since our model is physically derived, we may also estimate sensible ranges for the model parameters, reducing the number of parameters in the electric-circuit models which must be fitted to data.
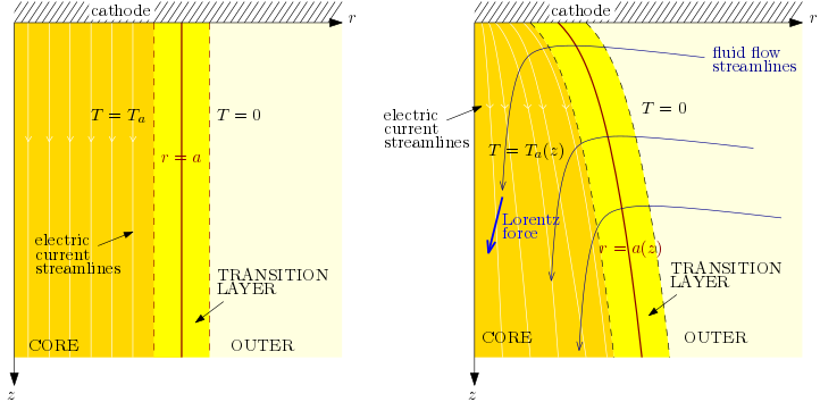
Figure 3: Schematics for the possible asymptotic structures of an electric arc, with conduction effects dominating over convection (left), and both convection and conduction effects important in determining the radial extent of the arc (right).
While our simple arc model has several benefits over the currently-used empirical models, it predicts a slightly too rapid decrease in the electrical resistance as the arc heats up. We hypothesise that this is because we have neglected the convection of heat from the simplified model. A more-detailed asymptotic analysis of the MHD arc model is ongoing work, using the method of matched asymptotic expansions. While heat radiation remains the dominant heat-loss mechanism, the size of the arc region is determined by either the conduction or the convection effects at the boundary, depending on the magnitude of the applied current. Schematics of the possible arc structure when conduction (left) and convection (right) effects determine the radial extent of the arc are shown in Figure 3. Through this asymptotic analysis, we hope to gain deeper understanding of how the coupled processes within electric arcs interact, and develop improved arc models for use in the electric models for the silicon furnace.
This work has been funded through the EPSRC Industrially Focused Mathematical Modelling Centre for Doctoral Training (InFoMM) in collaboration with Elkem ASA. Ellen Luckins is a Postdoctoral Research Associate in the Oxford Centre for Industrial and Applied Mathematics (OCIAM).