Solutions
Part of the Oxford MAT Livestream
These are the solutions for the Integration & Differentiation worksheet.
Warm-up
- Differentiate $x^{17}-x^{-17}$ with respect to $x$.
- The derivative of $x^a$ is $ax^{a-1}$ so the derivative of this expression is $17x^{16}+17x^{-18}$.
- Differentiate $2\sqrt{x}+3\sqrt[3]{x}$ with respect to $x$.
- Remember that $\sqrt{x}=x^{1/2}$ and $\sqrt[3]{x}=x^{1/3}$, so the derivative of this expression is $x^{-1/2}+x^{-2/3}$, which we could write as \(\frac{1}{\sqrt{x}}+\frac{1}{x^{2/3}}\) if we wanted to.
- Differentiate $1-e^{3x}$ with respect to $x$.
- Remember that the derivative of a constant is $0$, so the derivative of this expression is just $-3e^{3x}$.
- Find the tangent to the curve $y=e^x+x^2$ at $x=2$.
- We need to find the value of the derivative $\frac{\mathrm{d}y}{\mathrm{d}x}$ at $x=2$ because that's equal to the gradient of the tangent. We can differentiate to find $\frac{\mathrm{d}y}{\mathrm{d}x}=e^x+2x$ so that gradient we wanted is $e^2+4$. We also want the tangent to have the same value at $x=2$ as the curve; that's $e^x+x^2$ at $x=2$, which is also $e^2+4$. So our tangent is $y=(e^2+4)(x-1)$.
- Find the normal to the parabola $y=x^2$ at $x=3$.
- First find the derivative at $x=3$, which is $6$ for this parabola. That's the gradient of the tangent, and the normal is at right-angles to the tangent, so it has gradient $-\frac{1}{6}$. We have $y=-\frac{x}{6}+c$ and we want the normal to go through the point $(3,9)$. So we want $c=\frac{19}{2}$.
- Find the turning points of the curve $y=x^4-2x^3+x^2$. Identify whether the turning points are maxima or minima. For which values of $x$ is $y=x^4-2x^3+x^2$ increasing? For which values of $x$ is it decreasing?
- The turning points must have $\frac{\mathrm{d}y}{\mathrm{d}x}=0$ so we must have $4x^3-6x^2+2x=0$. That happens when $x=0$ or when $2x^2-3x+1=0$ which happens when $(2x-1)(x-1)=0$, which is either $x=1$ or $x=\frac{1}{2}$.
- Now find the second derivative to check whether these are minima or maxima. $\frac{\mathrm{d}^2y}{\mathrm{d}x^2}=12x^2-12x+2$, which is positive for $x=0$, negative for $x=\frac{1}{2}$, and positive for $x=1$. So we have a (local) minimum, then a (local) maximum, then a (local) minimum.
- The function is decreasing for $x<0$, then increasing for $0<x<\frac{1}{2}$, then decreasing for $\frac{1}{2}<x<1$ then increasing for $x>1$.
- Two points $A$ and $B$ are on the curve $y=x^3+x^2+x+1$. $A$ is fixed at $(1,4)$. The point $B$ moves along the curve towards $A$. What happens to the line through $A$ and $B$?
- The line definitely goes through $A$, which doesn't move. The thing we learn from "differentiation from first principles" is that the gradient of the line gets closer and closer to the derivative of the function at $A$.
- The derivative is $3x^2+2x+1$ which is 6 at $x=1$. The value is $4$, so the tangent is $y=6x-2$. So if the line through $A$ and $B$ is $y=mx+c$ then $m$ gets closer and closer to 6 and $c$ gets closer and closer to $-2$.
- Suppose that the derivative of a polynomial $p(x)$ with respect to $x$ is $q(x)$. Find an expression for $\displaystyle \int q(x)\,\mathrm{d}x$.
- This must be $p(x)+c$ for some constant $c$.
- Find the area enclosed between the polynomial $y=x^2+4x+3$ and the $x$-axis.
- First find the points where $y=0$. We have $(x+3)(x+1)=0$ so these points are at $x=-1$ or $x=-3$. In between, we have $y<0$ (by considering the graph).
- So we want $-\displaystyle \int_{-3}^{-1} x^2+4x+3\,\mathrm{d}x$. That minus sign out the front is because the function is negative.
- This works out to be $\frac{4}{3}$.
- Find $\displaystyle \int_{-1}^1 1+x+x^2+x^3+x^4+x^5+x^6\,\mathrm{d}x$.
- This is $\left[x+\frac{x^2}{2}+\frac{x^3}{3}+\frac{x^4}{4}+\frac{x^5}{5}+\frac{x^6}{6}+\frac{x^7}{7}\right]_{-1}^1=2+\frac{2}{3}+\frac{2}{5}+\frac{2}{7}=\frac{352}{105}$.
- Find $\displaystyle \int_{-\pi}^{\pi} x^{1729}\,\mathrm{d}x$.
- This is $\left[\frac{x^{1730}}{1730}\right]_{-\pi}^{\pi}=0$. In general, any "odd function" with $f(-x)=-f(x)$ which we integrate from $-a$ to $a$ for any real number $a$ will give zero.
- Find \[\int \frac{x+3}{x^3}\,\mathrm{d}x, \qquad \int \sqrt[3]{x}\,\mathrm{d}x,\qquad \int \left(\left(x^2\right)^3\right)^5\,\mathrm{d}x,\qquad \int \left(x^2+1\right)^3\,\mathrm{d}x\]
- $\displaystyle \int \frac{x+3}{x^3}\,\mathrm{d}x=\int \frac{1}{x^2}+\frac{3}{x^3},\mathrm{d}x=-\frac{1}{x}-\frac{3}{2x^2}+c$ where $c$ is a constant.
- $\displaystyle \int \sqrt[3]{x}\,\mathrm{d}x=\int x^{1/3}\,\mathrm{d}x=\frac{3}{4}x^{4/3}+c$ where $c$ is a constant.
- $\displaystyle \int \left(\left(x^2\right)^3\right)^5\,\mathrm{d}x=\int x^{30}\,\mathrm{d}x=\frac{x^{31}}{31}+c$ where $c$ is a constant.
- $\displaystyle \int \left(x^2+1\right)^3\,\mathrm{d}x=\int x^6+3x^4+3x^2+1\,\mathrm{d}x=\frac{x^7}{7}+\frac{3x^5}{5}+x^3+x+c$ where $c$ is a constant.
- By thinking about the area that the integral represents, explain why \[\int_{-1}^1 f(x)\,\mathrm{d}x=\int_{-1}^1 f(-x)\,\mathrm{d}x.\]
- The graph of $f(-x)$ is the graph of $f(x)$ reflected in $y$-axis. Also, note that if we reflect the interval $-1\leq x \leq 1$ in the $y$-axis then we get the same interval back. On the left-hand side, we're finding the area under $f(x)$ (or maybe negative the area in any regions where $f$ is negative). On the right-hand side, we're calculating exactly the same area, but with the shape of the graph reflected.
MAT questions
MAT 2014 Q1C
- First work out the derivative \(3kx^2-2(k+1)x+(2-k)\) and then the second derivative \(6kx-2(k+1)\).
- At $x=1$, the first derivative is \(3k-2(k+1)+(2-k)\), which is zero for any $k$, and the second derivative is \(6k-2(k+1)=4k-2\).
- For this to be a local minimum we would need zero derivative (which we have!) and we would need the second derivative to be positive, so we would need $k>\frac{1}{2}$.
- The answer is (c).
MAT 2017 Q1A
- Let's look for the stationary points by working out the derivative $6x^2-2kx+2$.
- That's got two distinct roots if the discriminant $4k^2-48$ is positive, which happens if $k^2>12$.
- Technically we should probably check that the second derivative isn't zero at these points, but since the first derivative is a quadratic, it can only have zero derivative at a root if there's a single repeated root (which is not the case).
- The answer is (b).
MAT 2014 Q1J
- This question is tough. We're not going to work out what the function $f(x)$ is! We're just going to work out precisely the information $\int_{-1}^1 f(x)\,\mathrm{d}x$. Let's give that number a name (it is a number, not a function of $x$). I'm going to call it $A$.
- Now the equation we've been given is \[6+f(x)=2f(-x)+3Ax^2\]
- I don't know much about $f(x)$, and frankly I don't care much about the details of $f(x)$, I just want to find $A$. I've noticed that if I integrate the left-hand side of the equation, I get $12+A$.
- If I integrate the right-hand side I get \[2\int_{-1}^1f(-x)\,\mathrm{d}x+3A\int_{-1}^1 x^2\,\mathrm{d}x.\] I've moved the $A$ outside of the integral there because it's just a constant.
- Now note that $\int_{-1}^1 f(-x)\,\mathrm{d}x=\int_{-1}^{1}f(x)\,\mathrm{d}x$; we talked about this in the warm-up. That's $A$.
- So we have $12+A=2A+3A\int_{-1}^1x^2\,\mathrm{d}x$. We're almost done, I just need to calculate one integral and I'll get an equation for $A$.
- I get $12+A=2A+2A$ so $A=4$.
- The answer is (a).
MAT 2016 Q1H
- First, let's calculate the two areas in the question.
- The $x$-axis and $f(x)$ enclose a region with $-\sqrt{a}<x<\sqrt{a}$ where $f(x)$ is positive. The area is \[\int_{-\sqrt{a}}^{\sqrt{a}}a-x^2\,\mathrm{d}x=2a^{3/2}-\frac{2}{3}a^{3/2}=\frac{4}{3}a^{3/2}.\]
- The $x$-axis and $g(x)$ enclose a region with $-a^{1/4}<x<a^{1/4}$ where $g(x)$ is negative. The area is \[-\int_{-a^{1/4}}^{a^{1/4}}x^4-a\,\mathrm{d}x=-\frac{2}{5}a^{5/4}+2a^{5/4}=\frac{8}{5}a^{5/4} \].
- We want to find out when the first area is bigger. We need \[\frac{4}{3}a^{3/2}>\frac{8}{5}a^{5/4}.\]
- This rearranges to $a>\left(\frac{6}{5}\right)^4$.
- The answer is (e).
MAT 2017 Q3
(i) Here's a sketch
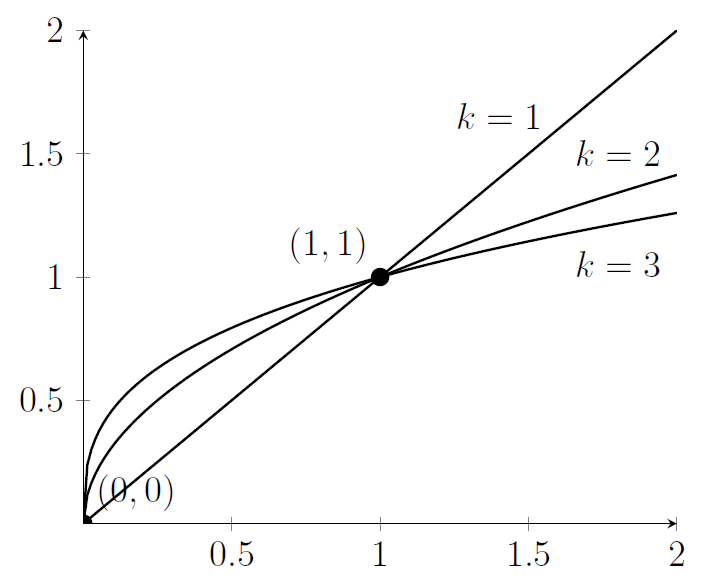
Note that all the curves pass through the point $(0,0)$ and through $(1,1)$. For $0<x<1$ the curve with the highest value of $k$ is the largest, but for $x>1$ the curve with the lowest value of $k$ is the largest.
(ii) For $0<x<1$, the curve $y=f_{k+1}(x)$ has a larger value than the curve $y=f_k(x)$. The area we want is \[\int_0^1 f_{k+1}(x)-f_k(x)\,\mathrm{d}x=\int_0^1 x^{1/(k+1)}-x^{1/k}\,\mathrm{d}x=\left[\frac{x^{1+1/(k+1)}}{1+1/(k+1)}-\frac{x^{1+1/k}}{1+1/k}\right]_0^1=\frac{k+1}{k+2}-\frac{k}{k+1}.\]
We can check that if $k=1$ then this is $\frac{2}{3}-\frac{1}{2}=\frac{1}{6}$.
(iii) Remember that $y=f_1(x)$ is just $y=x$. This intersects the line $y=c$ for $x=c$, so the point of intersection is $(c,c)$. The curve $y=f_2(x)$ is just $y=x^{1/2}$ so the point of intersection with the line $y=c$ is $(c^2,c)$.
(iv) Here's a sketch
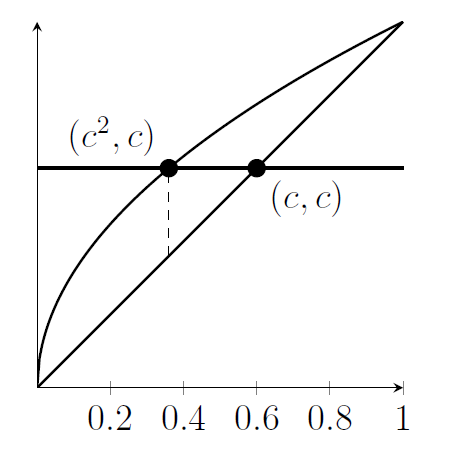
We can write the area between the curves and under $y=c$ in two parts as \[ A=\int_0^{c^2} x^{1/2}-x\,\mathrm{d}x+\int_{c^2}^c c-x\,\mathrm{d}x.\]
We can calculate these integrals to get (after simplifying) \[ A=\frac{c^2}{2}-\frac{c^{3}}{3}.\]
Now for the two regions to have equal area, they must each have area $\frac{1}{12}$, because we found in part (ii) that the overall area is $\frac{1}{6}$. This gives the equation $\frac{1}{12}=\frac{c^2}{2}-\frac{c^3}{3}$ which we can rearrange for $4c^3-6c^2+1=0$.
We know that $0<c<1$, so let's try guessing simple fractions as roots of this cubic. It turns out that $c=\frac{1}{2}$ works. Perhaps we could factorise the cubic to check that this is the only root in that range, but it's easier to argue geometrically; as $c$ increases from zero to one, the area under the line $y=c$ only increases, so we can't have two different values of $c$ which split the region in half.
Reflection
- Splitting the area up into multiple parts is a good tactic. In the long question, I split the area up into a region to the left of a point of intersection and a separate region to the right. I could have spotted that the region to the right was just a right-angled isosceles triangle, which might have been a faster way to get the area.
- If you've never seen something like $\int_{-1}^{1}f(t)\,\mathrm{d}t$ before, it's worth thinking about what this means and why it's the same thing as $\int_{-1}^{1}f(x)\,\mathrm{d}x$.
- Drawing sketches is still important, even if the question doesn't ask you to!

