Solutions
Part of the Oxford MAT Livestream
These are the solutions for the Recursion worksheet.
Warm-up
- A sequence is defined by \(a_0=3\) and then for \(n\geq 1\) \(a_n\) is the sum of all previous terms. Find \(a_n\) in terms of \(n\) for \(n\geq 1\).
- First note that \(a_1=3\) (the only previous term is 3) and then \(a_2=3+3=6\). After that, \(a_3=6+3+3=12\) and it seems like the terms double each time.
- That's true because \(a_{n}=a_{n-1}+a_{n-2}+\dots+a_0\) and \(a_{n-1}=a_{n-2}+\dots+a_0\) so \(a_{n}=a_{n-1}+a_{n-1}=2a_{n-1}\).
- So after \(a_0\) this is a geometric sequence with \(a_n=3\times 2^{n-1}\) for \(n\geq 1\).
- The Fibonacci numbers are defined by \(F_0=1\) and \(F_1=1\) and then for \(n\geq 2\), \(F_{n}=F_{n-1}+F_{n-2}\). Find \(F_{10}\).
- Let's calculate!
- \(F_2=F_1+F_0=1+1=2\).
- \(F_3=F_2+F_1=2+1=3\).
- \(F_4=F_3+F_2=3+2=5\).
- \(F_5=F_4+F_3=5+3=8\).
- \(F_6=F_5+F_4=8+5=13\).
- \(F_7=F_6+F_5=13+8=21\).
- \(F_8=F_7+F_6=21+13=34\).
- \(F_9=F_8+F_7=34+21=55\).
- \(F_{10}=F_9+F_8=55+34=89\).
- Suppose that we're trying to form a discussion group of \(r\) people from a wider collection of \(n\) people, one of whom is Sophie Germain. We'll write \(f(n,r)\) for the number of different groups we can form. By considering separate cases for discussion groups that do or do not contain Sophie Germain, explain why \[f(n,r)=f(n-1,r)+f(n-1,r-1)\]
- There are two possibilities; either Sophie Germain is in the discussion group, or she is not. These are mutually exclusive and cover all the possibilities (she's either in the group or she is not, not both of those and not neither).
- In the first case, Sophie Germain is in the discussion group. The group contains \(r-1\) more people chosen from the remaining \(n-1\) people who aren't Sophie Germain. The number of different groups like that is \(f(n-1,r-1)\). We can take any one of those groups and add Sophie Germain to make a group of \(r\) people.
- In the other case, Sophie Germain is not in the discussion group. The group must contain \(r\) people chosen from the remaining \(n-1\) people who aren't Sophie Germain. The number of different groups of \(r\) people chosen from \(n-1\) people is \(f(n-1,r)\).
- Since the two cases are mutually exclusive, we should add together the number of groups with Sophie with the number of groups without Sophie Germain. This gives the expression we're looking for.
- A sequence is defined by \(C_0=1\) and then for \(n\geq 0\), \[\displaystyle C_{n+1}=\sum_{i=0}^{n}C_iC_{n-i}.\] Find \(C_1\) and \(C_2\) and \(C_3\) and \(C_4\).
- For \(C_1\) I'll put \(n=0\) into the equation, so that the left-hand side reads \(C_1\). The right-hand side is then \[\sum_{i=0}^0 C_iC_{-i}.\] That looks pretty weird written out like that; the sum from \(i=0\) to \(0\) is just the term with \(i=0\), which is \(C_0^2\). So \(C_1=C_0^2=1\).
- Now for \(C_2\), I'll put \(n=1\) into the equation. The right-hand side is more interesting now; I get \[\sum_{i=0}^1C_iC_{1-i}\] which is \(C_0C_1+C_1C_0\). So \(C_2=C_0C_1+C_1C_0=2\).
- Then \(C_3=C_2C_0+C_1C_1+C_0C_2=5\) and \(C_4=C_3C_0+C_2C_1+C_1C_2+C_0C_3=14\).
MAT questions
MAT 2014 Q5
(i) We've got to start with A, and then we can have another A or go to B. In the first case, we can follow that with another A or switch to B for the third letter. In the second case, we can go back to A, use another B, or introduce C. So the five possibilities are AAA, AAB, ABA, ABB, ABC.
(ii) \(c_{n,1}\) is the number of rhyme schemes that have \(n\) lines and only use one letter. That's just a string of A's, so there's only one possibility. So \(c_{n,1}=1\).
\(c_{n,n}\) is the number of rhyme schemes that have \(n\) lines and use \(n\) letters. That means there's a new letter on each line, and so this is just the first \(n\) letters of the alphabet in a string; there's only one possibility, so \(c_{n,n}=1\).
(iii) We're working out \(c_{n,k}\) which is the number of rhyme schemes for a poem with \(n\) lines using exactly \(k\) letters. We're asked to think about the last line, so let's consider the possible cases. We've got to use \(k\) letters, and maybe this last line is the first and only time we used the \(k^\text{th}\) letter. If that's the case then the previous bit of poem didn't use that letter (that's a ``smaller" problem with fewer lines and fewer letters). What if, instead, the last letter is a repeat? Well, that case has several different possibilities, depending on how many letters we've previously used; that's how many options there are for the last letter in this case.
So in the first case, we'll use a poem with \(n-1\) lines and \(k-1\) letters, and then add a new letter right at the end to make a poem with \(n\) lines and \(k\) letters. In the second case, we'll use a poem with \(n-1\) lines and \(k\) letters, and then we'll have a choice of \(k\) letters for the last one to be a repeat of a previous letter.
Overall then, the number of possibilities is \(c_{n-1,k-1}+k\times c_{n-1,k}\) where the first term before the \(+\) is the first case (last letter is new) and the second term is the second case (last letter is a repeat of one of the previous letters).
(iv) \(r_n\) is the overall number of rhyme schemes using any number of letters, so \[r_n=c_{n,1}+c_{n,2}+c_{n,3}+\dots+c_{n,n-1}+c_{n,n}\]
So \(r_4=c_{4,1}+c_{4,3}+c_{4,2}+c_{4,1}\). We know that \(c_{4,1}=1\) and \(c_{4,4}=1\). For the other two terms, I'll use the fact from part (iii). I have \(c_{4,2}=2\times c_{3,2}+c_{3,1}\) and \(c_{4,3}=3\times c_{3,3}+c_{3,2}\). I'll tidy this up with \(c_{3,1}=1\) and \(c_{3,3}=1\). So \(r_4=6+3c_{3,2}\). We were told that \(c_{3,2}=3\) in the question, and we also worked those out (we found the three rhyme schemes AAB, ABA, ABB above). So \(r_4=15\).
(v) We could use the previous formula. That gives \(c_{n,2}=2\times c_{n-1,2}+c_{n-1,1}\), and we also know that \(c_{n-1,1}=1\) (for \(n\geq 2\)). So \(c_{n,2}=2\times c_{n-1,2}+1\). If I work out the first few terms with this rule, I get \(c_{2,2}=1\) then \(c_{3,2}=2\times 1+1=3\) and \(c_{4,2}=2\times 3+1=7\) and I can guess (and check) that \(c_{n,2}=2^{n-1}-1\).
Alternatively, and more directly, I can try to count how many rhyme schemes there are with \(n\) lines and two letters (just A and B). I've got to start with an A, and then I can use either an A or a B for the other \(n-1\) lines (so \(2^{n-1}\) possibilities), except I've got to have at least one B; I'm not allowed just A's, so I need to subtract one because AAAAA...AAA is not allowed. So the answer is \(2^{n-1}-1\).
MAT 2016 Q7
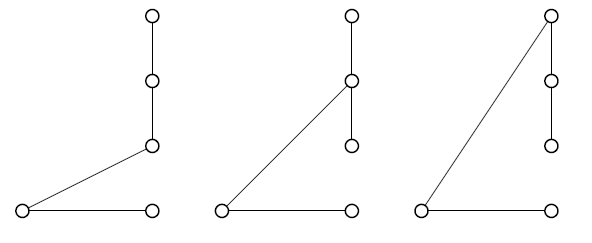
(i) There's a lot to think about and understand before we can get started with this. The definition of a 2-span involve a 2-fan, so let's think about that first. That consists of two points in a line, with a hub off to one side. I'll draw mine like the ones in the question.
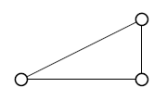
Now a 2-span is a subset of that with all the points and just 2 of the lines. All the points need to be connected to each other... but actually I can see that there are only three ways to choose 2 of the lines to keep. So I can just draw the three different ways to take a subset of 2 lines of the 2-fan.

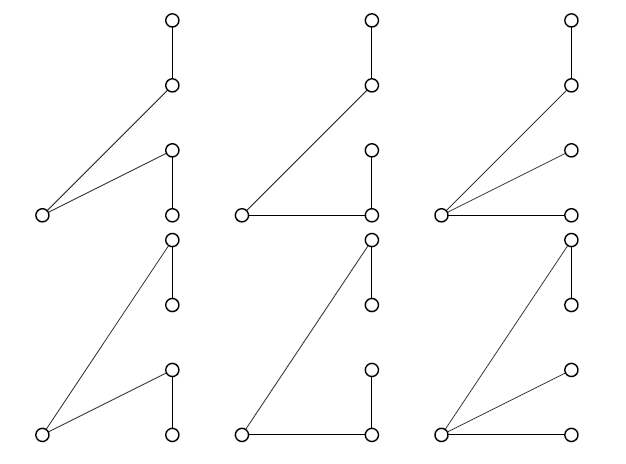
(ii) I'm not told how many 3-spans there are. Let's draw a 3-fan first just to think about what we're taking subsets of.
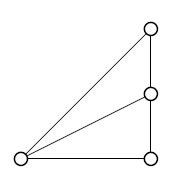
We want to choose 3 of those lines so that all the points are connected together, with a unique path between any two points. One way to work systematically through the possibilities is to think about whether the top tip is connected to the hub or not. If it isn't, then the top tip must be connected to the next tip down. If it is connected to the hub, then it might also be connected to the next tip down or it might not. That gives three sub-problems that we can work on where we've drawn in the top part of the 3-span. It turns out that there are only eight possibilities.
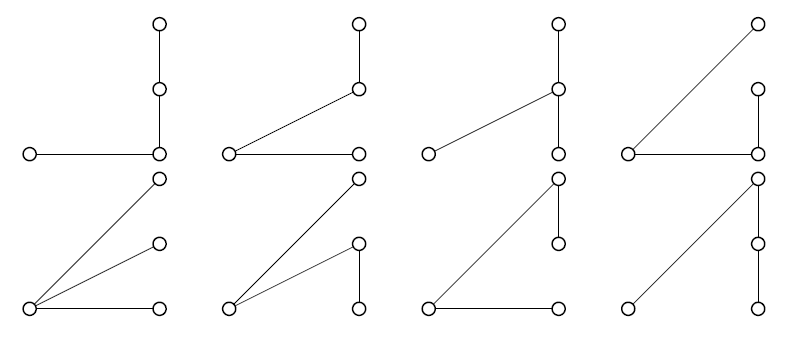
(iii) The top group of tips could include all four of the tips, or just three, or two, or one. In the first case, the points are all connected together, and there's exactly one line left to connect this group to the hub. This could be connected to any one of the four tips.
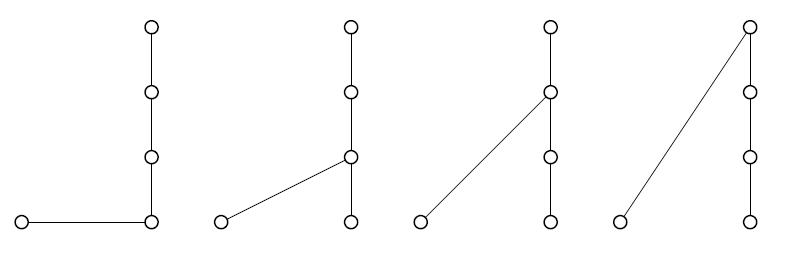
In the second case, there's a group of three at the top. The other tip must be connected to the hub (not to this group, otherwise it would be a group of four tips), and then there are three choices for how we connect the group of 3 to the hub.
In the third case, the top group has two tips. We can't connect the next tip to this group (otherwise it would be a group of three) so this group must connect to the hub somehow. There are two ways we could do that; join the top tip to the hub or join the second tip to the hub. But not both, otherwise there would be a complete triangle at the top, and there would be more than one path between the top tip and the hub. Separately, we've got to use two more lines to connect the other two tips to the hub... and that's precisely the problem of drawing all the possible 2-spans! We know there are three ways to do that, so overall in this case we've got six possibilities.
Finally, if the top group is just one tip then we must connect it to the hub and use three lines to connect the other three tips to the hub. That's the same as constructing all the possible 3-spans down here, so there are eight possibilities.
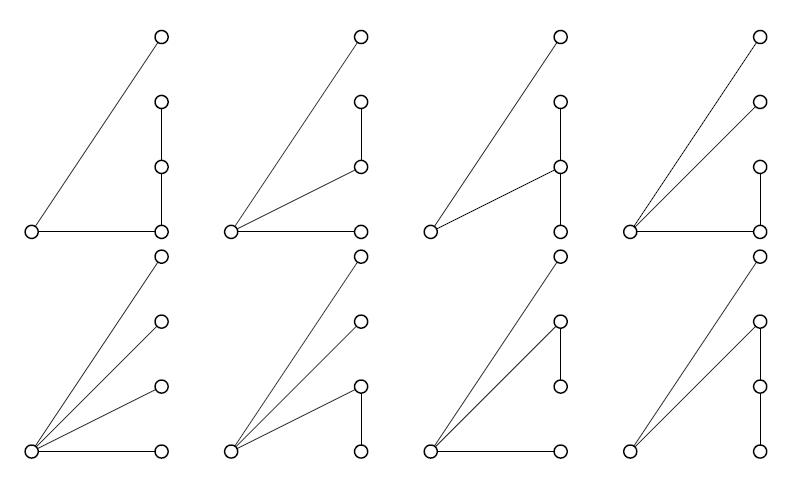
Overall, that makes \(4+3+6+8=21\).
(iv) Thinking in the same way as in part (iii), we can look at different cases for the size of the top group. If \(i\) tips are in that top group, then there are \(i\) choices of how that group is connected to the hub (it must be connected to the hub, not the next tip down, and connected to exactly one of the tips so that there's a unique path from the hub to any tip). Then we've reduced the problem to thinking about how to connect the other \(n-i\) tips to the hub, and the number of ways to do this is \(z_{n-i}\). Just like in part (iii), we can make the choice for how to join the top group separately from the choice of which \((n-i)\)-span to use, and we should consider all the possibilities for how large the top group is, with \(1\leq i \leq n\).
That idea lets me write down the expression \[z_n=1\times z_{n-1}+2\times z_{n-2}+3\times z_{n-3}+\dots + (n-1)\times z_1+n\times z_0.\]
I suppose \(z_0\) isn't really defined in this question, so perhaps for that last term I should say ``\(n\) ways to connect the group of size \(n\) to the hub, and then you're done". I could define \(z_0=1\) to achieve the same effect.
I'm asked to calculate \(z_5\) and I'll need to use the fact that \(z_1=1\) and all the other cases we worked on in parts (i) and (ii) and (iii). \[z_5=1\times z_4+2\times z_3+3\times z_2+4\times z_1+5\times z_0=21+2\times 8+3\times 3+4\times 1+5=55.\]
(v) Now in just the same way \[z_6=1\times z_5+2\times z_4+3\times z_3+4\times z_2+5\times z_1+6\times z_0=55+2\times 21+3\times 8+ 4\times 3+ 5\times 1 + 6=144.\]
Reflection
- It's really important to keep track of the different cases. Some people like to draw branching tree structures of the different cases and sub-cases. Some people like to label the cases. Some people like to explain first what the process is and then go through all the cases. The key thing is to work systematically. Finding that system is sometimes the main part of the problem, so don't panic if you can't immediately see how to split into cases; finding a sensible way to break down the problem is hard work.
- Sometimes there's a nice neat formula for what the answer is, and sometimes we just get an expression relating the number to previous terms in the sequence, and we're forced to calculate all the way up from 1. That's normal; some of the problems you'll meet have neat answers and some of them really really don't.

