Compressed Sensing Reconstruction of Dynamic X-Ray Imaging
 Researcher: Joseph Field
Researcher: Joseph Field- Academic Supervisors: Raphael Hauser and Andrew Thompson
- Industrial Supervisors: Paul Betteridge and Gil Travish
Background
Medical imaging techniques are key diagnostic tools in many areas of healthcare, and are vital for disease detection and for patient monitoring during ongoing care. A crucial development in X-ray imaging is digital tomosynthesis (DTS), in which a 3D image is reconstructed from a set of separately-captured 2D measurements. Standard DTS acquisition methods involve a single X-ray tube and a paired flat-panel detector, which are computer-controlled to move along predefined paths. 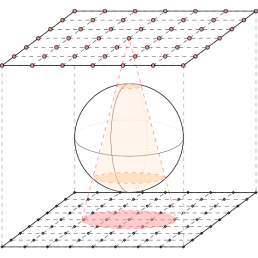
Adaptix, a British medical technology company, have instead developed a portable, low-cost X-ray source consisting of multiple low-power emitters arranged in an array. With this device it is possible to quickly fire a sequence of low-dose X-rays, such that the total radiation dosage is only slightly more than a single standard X-ray.
During a complete firing sequence of the X-ray emitters there may be small body movements, either from fluctuations in a patient’s resting position, or from internal changes due to functions such as breathing. The 3D reconstructions may therefore be blurred, and so Adaptix wish to investigate the possibility of reconstructing images which have been affected by motion.
Progress
We have so far worked on correction methods for simple translational motion, i.e. allowing a body to move with constant velocity, finding that obtained reconstructions can still be extremely close to the ‘ground-truth’. Moreover, it has been found that by allowing the body to move during image acquisition then reconstructions can in fact be better than if the body were to remain stationary. For example, in Figure 1, we compare the reconstructions from a stationary body to a motion-corrected dynamic body.
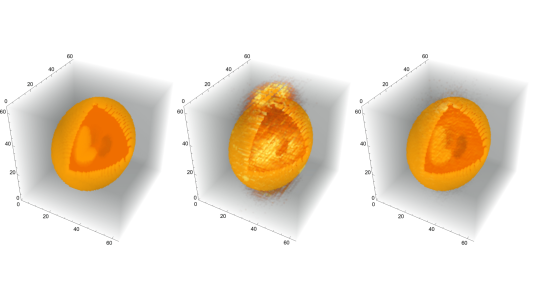
Figure 1. (Left) Shepp-Logan medical phantom at 64x64x64 resolution. (Middle) Reconstruction assuming that the body remains static during image acquisition. (Right) Reconstruction when allowing the body to move with constant velocity during the image acquisition.
Current work is focused on developing methods to find the true velocity to correct the reconstructions, under the assumption that if the true velocity is used in the correction scheme then this yields the most accurate reconstruction. Thus, we wish to optimise an error function - that is, we wish to find the velocity that minimises a chosen cost function – as efficiently as possible. For low spatial resolutions, e.g. a domain of 16x16x16 voxels, a good estimate for the minimising velocity can be obtained relatively quickly. Unfortunately, to find an accurate approximation of the true body velocity we must deal with linear systems of exponentially-increasing complexity, and so searching the velocity parameter space becomes a nontrivial task. With this in mind, we are exploring the use of simple optimisation methods, such as stochastic coordinate descent, as an initial approach for finding successively better approximations of the velocity.
Future Work
The approach for correcting constant velocity has been shown to work, but the computational cost required can be unreasonably large. That said, the same type of approach should be able to be used for bodies undergoing rotational motion, such that complete rigid motion can be corrected. As expected, the computational cost for such a problem will be much greater than our current problem and so future work must be spent on developing efficient ways for navigating the space of possible parameters, which for rigid motion is a subset of a 6-dimensional space.
A possible route of exploration is in the parallelisation of the computations necessary to build and solve the problem:
- To search the parameter space it is currently not efficient to use gradients, due to the time needed to approximate a single gradient value. However, finite difference evaluations are independent of one another, and so can be computed in parallel to obtain gradient approximation much faster, hopefully allowing for more efficient optimisation methods to become viable.
- Body motion is partitioned into distinct frames, which are all independent. Therefore, it is reasonable to assume that building each frame separately will speed up the total process. Similarly, within each frame, each ray is computed separately, so it could also be useful to parallelise this process too.
- It may even be possible to parallelise the method that we currently use for finding reconstructions, by lifting the problem to a higher dimension and solving directly in the Fourier domain. However, this approach may not be possible due to the size of our computations.

