Derivative-Free Algorithms for Nonlinear Optimisation Problems
Researcher: Lindon Roberts- Academic Supervisor: Coralia Cartis
- Industrial Supervisors: Jan Fiala and Benjamin Marteau
Background
Optimisation – that is, finding local maxima or minima of an ‘objective’ function – is one of the most common numerical tasks encountered in academia and industry. Almost all numerical methods for solving optimisation problems require the ability to compute derivatives of the objective function – these are used to determine both directions in which we expect the function to increase or decrease, and when to terminate the method. However, when the objective has stochastic noise or is expensive to compute, we may be unable to calculate or estimate derivatives.
Derivative-Free Optimisation (DFO) is the area of optimisation devoted to the development of algorithms which do not require any derivative information. Interest in DFO has been growing over the last 15-20 years. NAG, a British technology company, sells mathematical software via the NAG Library, and wishes to improve their current offering of DFO methods.
The aim of this project is to develop new DFO techniques in order to improve the performance of DFO for problems with stochastic noise, and large-scale problems.
Outcomes
A key part of this research was to improve existing DFO algorithms for nonlinear least-squares minimisation (where the objective function is a sum of squares of nonlinear functions). These problems are very common, and there are many applications where the objective is noisy or expensive, such as: data assimilation for weather and climate forecasting and parameter estimation for complex physical models.
We are using a new framework for building internal approximations of the objective, which improves on existing methods (typically based on polynomial interpolation) in two key ways. Firstly, it uses simpler approximations, similar to the classical Gauss-Newton method, which speeds up the algorithm substantially without sacrificing performance [1]. This simpler approach allows our algorithm to be more flexible, and it can begin the main optimisation procedure after as few as two objective evaluations (where most algorithms require at least as many evaluations as there are unknowns to be optimised). Secondly, we implement a variety of techniques to help the method make progress through noisy landscapes, including a novel multiple restarts mechanism which improves over existing techniques by being cheaper to implement and requiring fewer objective evaluations to make progress in its early stages [2].
For example, in Figure 1, we compare our new method (black/blue) against other state-of-the-art methods. We show the proportion of test problems solved for a given number of objective evaluations when we have added stochastic noise to the objective. Our method performs similarly for small computational budgets, but is much more robust, ultimately solving a greater proportion of the problems as the computational budget increases.
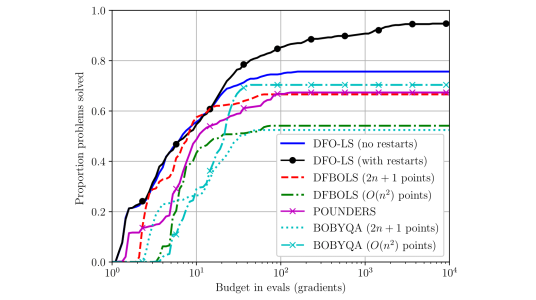
Figure 1: Comparison of two variants of our new method (DFO-LS in black and blue) to other state-of-the-art DFO solvers for problems (DFBOLS and POUNDERS for least-squares problems and BOBYQA for general objective problems).
We have taken several of these features for noisy problems and adapted them for general minimisation problems [2]. Further, we have shown that the multiple restarts mechanism can be modified to produce an algorithm that is effective at escaping local minima – that is, points which are optimal only compared to nearby points – and potentially finding global minima – points which are optimal compared to all other points – a much harder problem [3]. In Figure 2 below, we compare the proportion of test problems solved by our method for noisy problems (left), and a demonstration of its ability to escape local minima (right).
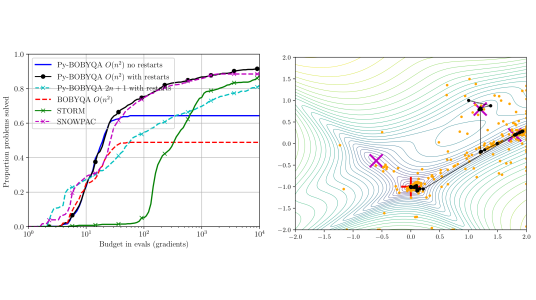
Figure 2: (left) Comparison of our method for general objective problems, Py-BOBYQA, against other state-of-the-art DFO methods for noisy problems (BOBYQA, STORM and SNOWPAC). We show the proportion of problems solved with a given number of objective evaluations; higher is better. (right) Path taken by Py-BOBYQA (black) and all evaluated points (orange) on a problem with several minima (purple, best minimum in red). Py-BOBYQA initially finds a suboptimal minimum near the starting point, but with our restarts mechanism is able to find other local minima, and it converges to the global solution.
Lastly, we have developed an algorithm for large-scale least-squares problems (i.e. problems with many unknowns to be optimised). These problems arise in areas such as weather forecasting and machine learning, but derivative-free methods have not been used in this setting, as their computational cost grows too quickly with problem size. We have addressed this by developing a method which optimises only a subset of variables at each iteration (but changing which subset each time), allowing the computational cost of the algorithm to be reduced. Our method allows larger problems to be solved within a given runtime (when objective evaluations are cheap), while also being able to make progress with few objective evaluations (when evaluations are expensive).
Two of our software packages have been publicly released: DFO-LS for least-squares problems and Py-BOBYQA for general objective problems. These algorithms have been implemented in Mark 27 of the NAG Library.
Publications
[1] Coralia Cartis and Lindon Roberts. A derivative-free Gauss-Newton method. Mathematical Programming Computation, (2019).
[2] Coralia Cartis, Jan Fiala, Benjamin Marteau and Lindon Roberts. Improving the flexibility and robustness of model-based derivative-free optimization solvers. ACM Transactions on Mathematical Software, to appear (2019).
[3] Coralia Cartis, Oliver Sheridan-Methven and Lindon Roberts. Escaping local minima with derivative-free methods: a numerical investigation. arXiv preprint arXiv:1812.11343, (2019).