Shape Optimisation with PDE and Geometric Constraints

• Researcher: Florian Wechsung
• Academic Supervisor: Patrick Farrell
• Industrial Supervisors: Mark Taylor

Background

Shape optimisation is concerned with design problems where the geometry of an object is to be
determined that minimises or maximises some objective. The relationship between the geometry and
the objective is typically governed by a PDE. Examples include: determining the optimal shape of a wing that
minimises the drag coefficient, while preserving its lift; determining the shape of a bridge of a given
mass that best supports its load; determining the bedrock shape beneath a glacier that explains its
observed motion. While shape optimisation has gained immense popularity in academia, there are several key issues that we will address in this project in order to bring the methodology to industrial relevance.

We use a technique known as shape calculus in order to find deformation vectorfields that morph a given initial shape into an optimal shape.

Outcomes

Fast solvers for the Navier-Stokes equations

In the case of aerodynamic and hydrodynamic shape optimisation, the PDE constraint is often given by some variant of the incompressible Navier–Stokes equations. A key parameter in these equations is the Reynolds number, a dimensionless quantity that measures the relative strength of inertial forces to viscous forces. At low Reynolds number, the flow is laminar and relatively straightforward to simulate; as the Reynolds number increases, the flow becomes more complex and the simulation difficulty increases accordingly. This latter regime is of particular interest since the simulation of high-Reynolds number flow is central to the design of aircraft, turbines, and cars.
A good solver for the linear systems arising in Newton’s method applied to these equations should have three properties: first, that its computational complexity scales linearly with the number of degrees of freedom (dofs); second, that it can be parallelised over many cores; and third, that its convergence does not degrade as parameters such as the Reynolds number are varied. It has proven difficult to develop solvers that enjoy all three properties. Matrix factorisations are robust to Reynolds number and are fast for small problems, but they scale badly with dof count and do not scale well to thousands of cores. Iterative methods using preconditioners such as PCD and LSC have complexity proportional to the problem size and scale well in parallel. However, both of these preconditioners rely on an approximation of the Schur complement and the quality of their approximation degrades as the Reynolds number is increased, leading to significant growth of iteration counts and eventual failure to converge.

We have developed an augmented Lagrangian type preconditioner [1] based on a custom multigrid method with linear complexity and iteration counts that only grow slightly with the Reynolds number. In addition, we have demonstrated that the algorithm scales well to more than 24,000 cores on ARCHER, the UK supercomputer.

Automated calculation of shape derivatives

In order to perform efficient optimisation over a large control space, the calculation of derivatives is crucial. In the case of shape optimisation, this itself poses a challenge, in particular when the objective is subject to a PDE constraint, as both the PDE and its solution change as the domain deforms. Applying the rules of shape calculus is often tedious and prone to error: even for simple objectives and constraints these calculations regularly span many pages in papers and dissertations on shape optimisation.

We have developed an extension to the Unified Form Language for automatically and symbolically deriving shape derivatives of a large class of integrals [2]. The key insight of this implementation is that a classical Gâteaux derivative with respect to the pull-back performed when assembling integrals over finite element functions is equivalent to shape differentiation. The approach is generic, extends to higher order derivatives, and makes shape optimisation easily accessible to users of the FEniCS and Firedrake finite element libraries. In particular, it enables rapid development of solvers for shape optimisation problems that are constrained by complicated, nonlinear PDEs such as the Navier–Stokes equations.

Mesh deformations

We create a mesh of the domain, in order to solve the PDE that governs the relationship between the geometry and the objective. Optimising for the shape of the domain then translates to moving the nodes of the mesh; here one needs to be careful that this deformation does not lead to overlapping or strong distortion of the mesh.
Stretched triangles as see in the left of the picture below can lead to numerical inaccuracy.

We have formulated new mesh deformation methods based on conformal mappings so that the mesh stays well behaved and we can avoid costly remeshing [4].

Left: Deformed geometry using classical deformation methods. We can see strongly stretched triangles in the area of high curvature. This leads to numerical inaccuracy in computations on this mesh. Right: Using nearly conformal mappings the mesh quality remains good throughout the optimisation.

Furthermore, in [3] we have explored the use of high-order methods to discretize deformation vectorfields.
High order methods offer higher accuracy and are desirable when shapes of higher regularity (e.g. without kinks) are required.

Geometric constraints

An important class of constraints are geometric constraints on the shape itself. Two classical and well understood examples for this are constraints on the volume or the location of the barycentre of the shape. Another requirement is that often the shape needs to be contained in a feasible region. This can be due to the existence of other parts in the design or because of regulations. For example, in Formula 1 the design of the each component of the car is strongly regulated by the FIA. Though this kind of constraint is crucial when trying to solve real world problems, it is usually only considered in the parametric case, e.g. by bounding the location of nodes of free form deformation boxes, and there is surprisingly little literature treating its inclusion in a continuous, non-parametric setting.

We have formulated an augmented Lagrangian method to incorporate such a constraint when the feasible region is given by a box and the method can be extended to general convex domains.

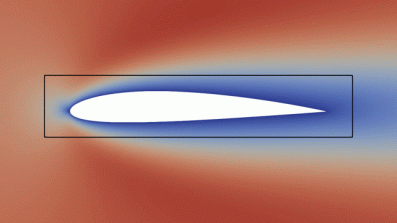
Above (click to see animation): We consider an airfoil and solve the Navier-Stokes equations. The objective to be maximised is the aerodynamic efficiency: the ratio of lift and drag. We furthermore impose the additional geometric constraint that the shape needs to be contained in the black box - this is similar to the bounding boxes that the wings of Formula 1 cars are subject to.

Publications

[1] Patrick E. Farrell, Lawrence Mitchell, and Florian Wechsung. "An Augmented Lagrangian Preconditioner for the 3D Stationary Incompressible Navier–Stokes Equations at High Reynolds Number", SIAM Journal on Scientific Computing, 2019.

[2] David A. Ham, Lawrence Mitchell, Alberto Paganini, and Florian Wechsung. "Automated shape differentiation in the Unified Form Language", Structural and Multidisciplinary Optimization, 2019.

[3] Alberto Paganini, Florian Wechsung, and Patrick E. Farrell. "Higher-order moving mesh methods for PDE-constrained shape optimization.", SIAM Journal on Scientific Computing, 2018.

[4] José A. Iglesias, Kevin Sturm, Florian Wechsung. "Shape optimisation with nearly conformal transformations" SIAM Journal on Scientific Computing, 2018.