Dupin Cyclides
Introducing Dupin Cyclides
Dupin cyclides were discovered by French mathematician Charles Dupin in 1882 [1]. They received much attention including works by Arthur Cayley and James Clerk Maxwell [2, 3]. A Dupin cyclide is characterised by the property that all of its lines of curvature are (arcs/segments of) either circles or lines. Mathematicians sometimes refer to this generalisation of a circle or line as a "circline". In a sense, this generalises the notion of a ruled surface (made up of straight lines) to surfaces made up of circlines. Also, a Dupin cyclide is a "channel surface", meaning it is an envelope of a certain family of spheres. Recall that an envelope of a family of spheres is a surface which is tangent to every sphere at some point. The spheres in question all have their centres lying along a (space) curve.
Cyclides and similar structures can be of interest to artists and architects [4]. An elegant sculpture by Florian Claar has some cyclide-like structure, as does this pavilion design. There are even cyclide-inspired chairs. See [5] to read some (advanced) material on the applications of Dupin cyclides in geometric modelling.
Construction
A Dupin cyclide is constructed by "inverting" (we shall make this notion more concrete later) a cylinder, cone, or standard torus in a sphere - see here for helpful images. These three surfaces are also Dupin cyclides themselves. As in other contexts, cylinders and cones are taken to be infinite, with cones consisting of two components meeting at their sharp ends. A standard torus means one swept out by a circle rotating about an axis, rather than the topological sense of any surface with one hole. More concretely, a standard torus can be parameterised by: $$ \begin{array}{c} x = ( R + r\cos\theta ) \cos\phi \\ y = ( R + r\cos\theta ) \sin\phi \\ z = r \sin\theta \end{array} $$
Standard tori fall into four categories. For $R>r, R=r, R<r$ we have respectively a familiar "ring torus", a "horn torus" with the rotating circle touching the axis of rotation, or a self-intersecting "spindle torus". A sphere is a degenerate case where $R=0$.
Naturally, lines of curvature are displayed on the models to illustrate their defining feature. One can see that on each model, if any two circles intersect then they intersect orthogonally (at right-angles). It was conjectured in 1986 by German mathematician Ulrich Pinkall that the only surfaces in $\mathbb{R}^3$ containing two such orthogonal families of circles are in fact Dupin cyclides [6]. This was proven in 1995 by American mathematician Thomas Ivey [7].
Inversion in a Sphere
From standard tori, more Dupin cyclides can be constructed by applying an "inversion in a sphere". To see what this map entails, consider a sphere of radius $r$, with (orthogonal) coordinates chosen such that the centre of the sphere is at the origin (note that the torus is not necessarily centred about the origin). In this coordinate system, we map points $(x, y, z)$ on the torus to $$r^2\frac{ (x, y, z)}{x^2 + y^2 + z^2}$$Note that this mapping is not well-defined at the origin $(0, 0, 0)$, but we rectify this by compactifying $\mathbb{R}^3$, which basically amounts to adding a "point at infinity". This inversion map has the important property that it maps lines of curvature on the given surface to lines of curvature on the new surface. Also circlines are mapped to circlines, so the defining feature of a Dupin cyclide is preserved under inversion in a sphere (i.e. if we invert a Dupin cyclide, we get another Dupin cyclide). Now let us explore the categorisation of the models.
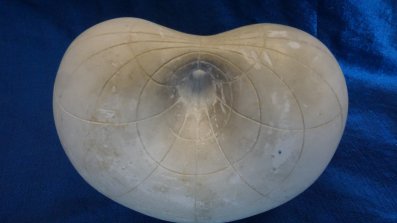
Ring Cyclides
Model IX 8 is a "ring cyclide", which is obtained by inverting a ring torus.
Model IX 9 is another ring cyclide, with different proportions to IX 8.
For a ring cyclide, if the centre of the sphere of inversion lies on the torus then it is called a "parabolic ring cyclide", which is demonstrated with model X 5. This model also has the interesting property that is splits up Euclidean space into two identical interlocking parts (i.e. it is congruent to itself - consider turning it upside down and rotating by 90 degrees). A fun upshot of this is that the mould used to cast the plaster model will have in fact been identical to the model itself. Ring cyclides and cylinders are the only non-singular Dupin cyclides.
Others
There are another two main classes of cyclide: spindle and horn. The classification of cyclides is not limited to these three cases though, as we will see with models IX 7, X 8a, X 8b - these are "general cyclides".
A "spindle cyclide" is obtained by inverting a spindle torus. Spindle cyclides can take very different shapes, depending on where the centre of the sphere of inversion lies. If the sphere's centre lies inside the torus, then the spindle cyclide looks very different. If the centre lies at a non-singular point on the torus, then we get a "parabolic spindle cyclide". There is also a degenerate case where the centre coincides with a singularity; this gives a cone.
A "horn cyclide" is obtained by inverting a horn torus. If the centre of the sphere of inversion lies on a non-singular point of the horn torus, then we have a "parabolic horn cyclide". Horn cyclides are singular. Given the thin neighbourhood of the singularity of a horn cyclide, their production in plaster was very difficult. Some illustrations will have to suffice. As with spindle cyclides, inverting in a sphere whose centre coincides with the singularity of a horn cyclide yields a cylinder.
Model IX 7 is a general cyclide with a double line, and is in fact a "cross-cap", which is a representation of the projective plane $\mathbb{P}^2$.
Model X 8a is a general cyclide, obtained by inverting a parabolic cylinder (a cylinder whose cross-section is a parabola rather than a circle). Many lines of curvature are displayed, elegantly demonstrating the defining property of a cyclide.
Model X 8b is another general cyclide exhibiting lines of curvature.
*video*
Interesting Properties
We finish this section by exploring some interesting properties and uses for Dupin cyclides.
In 1891, American mathematician Maxime Bôcher discovered an interesting means of solving Laplace's equation in $\mathbb{R}^3$, using cyclides to determine coordinate systems [8]. Solutions to Laplace's equation give rise to harmonic functions, which are important in many areas of science. For example, they accurately describe the behaviour of gravitational and electric potential. Dupin cyclides and similar objects are still being studied at the forefront of mathematical research. They are an object of great significance in the fascinating discipline of Lie sphere geometry [9], and the notion of Dupin cyclides can be extended to higher dimensions by "Dupin submanifolds", with their classification of particular interest [9]. For more on Dupin cyclides, there are many online resources. For instance, mathcurve.com has an excellent collection of images (with French notes).
References
[1] C. Dupin, Applications de géométrie et de méchanique à la marine, aux ... (1822), p200, http://gallica.bnf.fr/ark:/12148/bpt6k110325x
[2] Cayley, A., 1873. On the cyclide. Q. J. Pure Appl. Math. 12, 148–165.
[3] Maxwell, J.C., 1868. On the cyclide. Q. J. Pure Appl. Math. 9, 111–126.
[4] Rimas Krasauskas, Circular meshes, cyclide splines and geometric algebra, http://folk.uio.no/ranestad/krasauskas.pdf
[5] H.E. Bez, Bounded domain, bi-quadratic rational parametrizations of Dupin cyclides, http://www.tandfonline.com/doi/abs/10.1080/00207160701477476
[6] Gerd Fischer, Mathematical Models: Photograph Volume and Commentary
[7] Thomas Ivey, SURFACES WITH ORTHOGONAL FAMILIES OF CIRCLES, proceedings of the American Mathematical Society Volume 123, Number 3, March 1995
[8] M. Bôcher, Über die Reihenentwicklungen der Potentialtheorie (1891), http://www.worldcat.org/title/ueber-die-reihenentwicklungen-der-potenti…
[9] T.E. Cecil, Lie sphere geometry (1992), New York: Universitext, Springer-Verlag, ISBN 978-0-387-97747-8