G is for Growth Tensor
The Author

Prof Derek Moulton
Associate Professor in Mathematical Biology
Derek Moulton is a researcher in applied mathematics, focusing on mathematical modelling and applying computational and analytical tools to answer questions in the natural sciences, especially biology. His work is focused primarily on the continuum scale, and he is particularly interested in: mechanical biology and physiology, growth and pattern formation, morphoelasticity, and elastic mechanisms in nature.
Find out more
If you're interested in finding out more about Derek's research you can look at his website.
Nrich has a selection of biological and mathematical problems in their Preparing for University pages.
If you want to think about developing your own mathematical models you can take a look at the problems on Math Models.
There are several international competitions for mathematical modeling run by COMAP open to both school students and undergraduates: the Mathematical Contest in Modeling (MCM) and the Interdisciplinary Contest in Modeling (ICM).
"How does your garden grow?" is an article in Plus magazine about the developing field of theoretical biology, which uses formal mathematics to predict biological laws.
G is for Growth Tensor
A tree branch, a ram's horn, your hand - how have these distinct and consistent shapes come about? The growth and form of a biological entity is a complex matter that involves integrated activities across a number of length scales. Viewed at the scale of tissues, or large clusters of cells, understanding growth and form is a problem well suited for continuum mechanics and mathematical modelling.
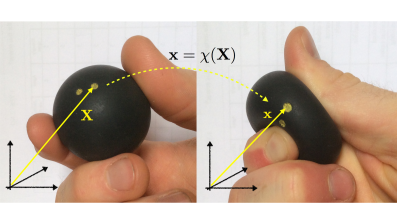
Within continuum mechanics, elasticity studies the deformation of objects that quickly return to their original shape once applied pressures are removed. For example, when you squeeze a rubber ball it deforms; when you let go it returns to a sphere. A starting point for describing mathematically the behaviour of an elastic object is to define a map from an unstressed reference state (e.g. the rubber ball as it sits in your hand) to a current state (the squeezed ball). Mathematically, if we denote material points in the reference state with position vector $\mathbf{X}$ and those in the current state with position vector $\mathbf{x}$, then there exists a one-to-one map $\chi$ between the two.
We then define the deformation gradient tensor as the gradient of this map, that is $\mathbf{F}=\frac{\partial{\mathbf{x}}}{\partial{\mathbf{X}}}$. Here $\mathbf{F}$ is a second order tensor (it maps vectors to vectors) that describes the local deformation (stretching, compressing, shearing) of the material, such that a small vector element $d\mathbf{X}$ in the reference state is deformed to $d\mathbf{x}=\mathbf{F}d\mathbf{X}$.
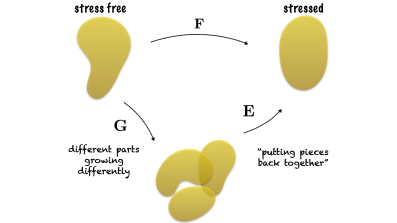
The above framework describes deformations of a body whose reference state remains unchanged, like a rubber ball. An elastic biological material, such as the tissue that makes up your hand, is also well described by the framework above, except that we must also take into account growth of the body. Growth, viewed at the continuum level, is simply a local increase (or decrease) in mass. To incorporate this in the description above, we decompose $\mathbf{F}$ as the product of two tensors:
$$\mathbf{F}=\mathbf{E}\mathbf{G},$$
where $\mathbf{E}$ is the elastic tensor and $\mathbf{G}$ is the growth tensor. Intuitively, each local element grows according to $\mathbf{G}$, and then $\mathbf{E}$ characterises the purely elastic response of the material, maintaining integrity of the body (no gaps or overlaps) and responding to external loads. This decomposition forms the key theoretical component of the field of morphoelasticity, a term coined by Oxford mathematician Alain Goriely.
One particularly important aspect of morphoelasticity is the notion of differential growth -- different rates of growth in different locations or directions. This idea underlies all the diversity of biological form: without differential growth, we would all be spheres! To see the impact mechanically, imagine a cylindrical body growing axially, i.e. lengthwise, such that the inside grows more quickly than the outside. A growth tensor for this could be
$$\mathbf{G}=(\beta - \alpha R)\mathbf{e}_z\otimes\mathbf{e}_z,$$
where $R$ is the radius, $\alpha, \beta>0$ are constants, and the tensor $\mathbf{e}_z\otimes\mathbf{e}_z$ reflects that growth is in the axial direction only.
Since $\mathbf{G}$ is non-homogeneous, the growth generates residual stress, which means that the body is in stress even without any applied pressure. You can observe residual stress on your own with a stalk of rhubarb. If you peel the rhubarb, you will notice that the outer layers become shorter, and the inner layer (the pith) becomes longer. This means that in the rhubarb stalk, the outer layers are in tension while the pith is in compression. Residual stress is critical to the structural properties of the rhubarb, and is an essential mechanical feature in many other systems as well. Developing tools to solve problems in morphoelasticity is an important area at the intersection of biology, mechanics, and mathematics.