Past

By a "coarse median" we mean a ternary operation on a path metric space, satisfying certain conditions which generalise those of a median algebra. It can be interpreted as a kind of non-positive curvature condition, and is applicable, for example to finitely generated groups. It is a consequence of work of Behrstock and Minsky, for example, that the mapping class group of a surface satisfies this condition. We aim to give some examples, results and applications concerning this notion.

Abstract: We study measures on half planar maps that satisfy a natural domain Markov property. I will discuss their classification and some of their geometric properties. Joint work with Gourab Ray.

A multi-dimensional extension of the structural default model with firms' values driven by diffusion processes with Marshall-Olkin-inspired

correlation structure is presented. Semi-analytical methods for solving

the forward calibration problem and backward pricing problem in three

dimensions are developed. The model is used to analyze bilateral counter- party risk for credit default swaps and evaluate the corresponding credit and debt value adjustments.

In many places, the Antarctic and Greenland ice sheets are fringed by tongues of ice floating on the ocean, called ice shelves. Recent observations and modelling suggest that melting and disintegration of the floating ice shelves can impact ice sheet flow, and hence have consequences for sea level rise. Of particular interest are observations of channels and undulations in the ice shelf base, for which the conditions for genesis remain unclear. To build insight into the potential for melting-driven instability of the ice shelf base, this talk will consider a free boundary problem with melting at the ice-ocean interface coupled to a buoyant plume of meltwater confined below a stationary ice shelf. An asymptotic model of turbulent heat transfer in the meltwater plume reveals that melting rates depend on ice-shelf basal slope, with potentially shocking consequences for the evolving ice-shelf geometry

In this talk I will explain a notion of p-adic functoriality for inner forms of definite unitary groups. Roughly speaking, this is a morphism between so-called eigenvarieties,  which are certain rigid analytic spaces parameterizing p-adic families  of automorphic forms. We will then study certain properties of classical Langlands functoriality that allow us to prove p-adic functoriality in some "stable" cases.

It is generally believed that in order to generate waves, a small object (like an insect) moving at the air-water surface must exceed the minimum wave speed (about 23 centimeters per second). We show that this result is only valid for a rectilinear uniform motion, an assumption often overlooked in the literature. In the case of a steady circular motion (a situation of particular importance for the study of whirligig beetles), we demonstrate that no such velocity threshold exists and that even at small velocities a finite wave drag is experienced by the object. This wave drag originates from the emission of a spiral-like wave pattern. The results presented should be important for a better understanding of the propulsion of water-walking insects. For example, it would be very interesting to know if whirligig beetles can take advantage of such spirals for echolocation purposes.

The Borel conjecture is one of the most important (and difficult) conjectures in Topology. We explain how some weaker but highly related conjectures are being tackled through the coarse geometry of finitely generated groups.

Central extensions of a finite group G correspond to 2-cocycles on G, which give rise to an abelian cohomology group known as the Schur

multiplier of G. Recently, the Schur multiplier was defined in a much more

general setting of a monoidal category. I will explain how to twist algebras by categorical 2-cocycles and will mention the role of

such twists the theory of quantum groups. I will then describe an approach to twisting rational Cherednik algebras by cocycles,

and will discuss possible applications of this new construction to the representation theory of these algebras.

Over million year time scales, the evolution and deformation of rocks on Earth can be described by the equations governing the motion of a very viscous, incompressible fluid. In this regime, the rocks within the crust and mantle lithosphere exhibit both brittle and ductile behaviour. Collectively, these rheologies result in an effective viscosity which is non-linear and may exhibit extremely large variations in space. In the context of geodynamics applications, we are interested in studying large deformation processes both prior and post to the onset of material failure.

\\

\\

Here I introduce a hybrid finite element (FE) - Lagrangian marker discretisation which has been specifically designed to enable the numerical simulation of geodynamic processes. In this approach, a mixed FE formulation is used to discretise the incompressible Stokes equations, whilst the markers are used to discretise the material lithology.

\\

\\

First I will show the a priori error estimates associated with this hybrid discretisation and demonstrate the convergence characteristics via several numerical examples. Then I will discuss several multi-level preconditioning strategies for the saddle point problem which are robust with respect to both large variations in viscosity and the underlying topological structure of the viscosity field.

\\

Finally, I will describe an extension of the multi-level preconditioning strategy that enables high-resolution, three-dimensional simulations to be performed with a small memory footprint and which is performant on multi-core, parallel architectures.

This paper analyzes a generalized class of flat-top realized kernels for

estimation of the quadratic variation spectrum in the presence of a

market microstructure noise component that is allowed to exhibit both

endogenous and exogenous $\alpha$-mixing dependence with polynomially

decaying autocovariances. In the absence of jumps, the class of flat-top

estimators are shown to be consistent, asymptotically unbiased, and

mixed Gaussian with the optimal rate of convergence, $n^{1/4}$. Exact

bounds on lower order terms are obtained using maximal inequalities and

these are used to derive a conservative MSE-optimal flat-top shrinkage.

In a theoretical and/or a numerical comparison with alternative

estimators, including the realized kernel, the two-scale realized

kernel, and a proposed robust pre-averaging estimator, the flat-top

realized kernels are shown to have superior bias reduction properties

with little or no increase in finite sample variance.

{\bf This seminar is at ground floor!}

\\

An important question in geometry and analysis is to know when two $k-$forms

$f$ and $g$ are equivalent. The problem is therefore to find a map $\varphi$

such that%

\[

\varphi^{\ast}\left( g\right) =f.

\]

We will mostly discuss the symplectic case $k=2$ and the case of volume forms

$k=n.$ We will give some results when $3\leq k\leq n-2,$ the case $k=n-1$ will

also be considered.

\\

The results have been obtained in collaboration with S. Bandyopadhyay, G.

Csato and O. Kneuss and can be found, in part, in the book below.\bigskip

\\

\newline

Csato G., Dacorogna B. et Kneuss O., \emph{The pullback equation for

differential forms}, Birkha\"{u}ser, PNLDE Series, New York, \textbf{83} (2012).

This is joint work with Angus Macintyre. We study model-theoretic properties of 
the ring of adeles, the hyperring of adele classes (studied by Connes-Consani), 
and residual hyperfields of valued fields (in the sense of Krasner).

I'll discuss work of Wise and Ollivier-Wise that gives cubulations of certain small cancellation and random groups, which in turn shows that they do not have property (T).

There appears to be no universally accepted rigorous definition of a "flexagon" (although I will try to give a reasonable one in the talk). Examples of flexagons were most likely discovered and rediscovered many times in the past - but they were "officially" discovered in 1939, a serendipitous consequence of the discrepancy between US paper sizes and sensible paper sizes.* I'll describe a couple of the most famous examples of flexagons (with actual models to play with of course), and also introduce some of the more abstract theory of flexagons which has been developed. Feel free to bring your own models of flexagons!

* The views expressed herein are solely those of the speaker, and do not reflect the official position of the Kinderseminar w.r.t. international paper standards. 

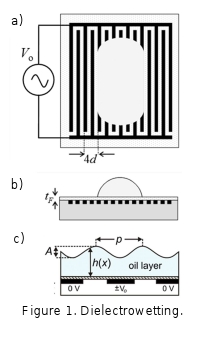The contact angle of a liquid droplet on a surface can be controlled by making the droplet part of a capacitive structure where the droplet contact area forms one electrode to create an electrowetting-on-dielectric (EWOD) configuration [1]. EWOD introduces a capacitive energy associated with the charging of the solid-liquid interface, in addition to the surface free energy, to allow the contact angle, and hence effective hydrophilicity of a surface, to be controlled using a voltage. However, the substrate must include an electrode coated with a thin, and typically hydrophobic, solid insulating layer and the liquid must be conducting, typically a salt solution, and have a direct electrical contact. In this seminar I show that reversible voltage programmed control of droplet wetting of a surface can be achieved using non-conducting dielectric liquids and without direct electrical contact. The approach is based on non-uniform electric fields generated via interdigitated electrodes and liquid dielectrophoresis to alter the energy balance of a droplet on a solid surface (Fig. 1a,b). Data is shown for thick droplets demonstrating the change in the cosine of the contact angle is proportional to the square of the applied voltage and it is shown theoretically why this equation, similar to that found for EWOD can be expected [2]. I also show that as the droplet spreads and becomes a film, the dominant change in surface free energy to be expected occurs by a wrinkling/undulation of the liquid-vapor interface (Fig. 1c) [3,4]. This type of wrinkle is shown to be a method to create a voltage programmable phase grating [5]. Finally, I argue that dielectrowetting can be used to modify the dynamic contact angle observed during droplet spreading and that this is described by a modified form of the Hoffman-de Gennes law for the relationship between edge speed and contact angle. In this dynamic situation, three distinct regimes can be predicted theoretically and are observed experimentally. These correspond to an exponential approach to equilibrium, a pure Tanner’s law type power law and a voltage determined superspreading power law behavior [6]. 

Acknowledgements

GM acknowledges the contributions of colleagues Professor Carl Brown, Dr. Mike Newton, Dr. Gary Wells and Mr Naresh Sampara at Nottingham Trent University who were central to the development of this work. EPSRC funding under grant EP/E063489/1 is also gratefully acknowledged.

References

[1]   F. Mugele and J.C. Baret, “Electrowetting: From basics to applications”, J. Phys.: Condens. Matt., 2005, 17, R705-R774.

[2]  G. McHale, C.V. Brown, M.I. Newton, G.G. Wells and N. Sampara, “Dielectrowetting driven spreading of droplets”, Phys. Rev. Lett., 2011, 107, art. 186101.

[3]  C.V. Brown, W. Al-Shabib, G.G. Wells, G. McHale and M.I. Newton, “Amplitude scaling of a static wrinkle at an oil-air interface created by dielectrophoresis forces”, Appl. Phys. Lett., 2010,  97, art. 242904.

[4]  C.V. Brown, G. McHale and N.J. Mottram, “Analysis of a static wrinkle on the surface of a thin dielectric liquid layer formed by dielectrophoresis forces”, J. Appl. Phys. 2011, 110 art. 024107.

[5]  C.V. Brown, G. G. Wells, M.I. Newton and G. McHale, “Voltage-programmable liquid optical interface”, Nature Photonics, 2009, 3, 403-405.

[6]  C.V. Brown, G. McHale and N. Sampara, “Voltage induced superspreading of droplets”, submitted (2012)

 One of the applications of the study of assymptotics of
homology groups in residually free groups of type FP_m is the calculation
of their analytic betti numbers in dimension up to m.

Exhibitors will be here along with recruiters from different sectors. There will also be panel talks. For further information see http://www.careers.ox.ac.uk/wp-content/uploads/2012/02/JobsForMathemati… and in particular last year brochure for the event at http://www.careers.ox.ac.uk/wp-content/uploads/2012/04/MathsPrintII.pdf

Let $Q_n$ denote the graph of the $n$-dimensional cube with vertex set $\{0, 1\}^n$

in which two vertices are adjacent if they differ in exactly one coordinate.

Suppose $G$ is a subgraph of $Q_n$ with average degree at least $d$. How long a

path can we guarantee to find in $G$?

My aim in this talk is to show that $G$ must contain an exponentially long

path. In fact, if $G$ has minimum degree at least $d$ then $G$ must contain a path

of length $2^d − 1$. Note that this bound is tight, as shown by a $d$-dimensional

subcube of $Q^n$. I hope to give an overview of the proof of this result and to

discuss some generalisations.