As part of our series of research articles focusing on the rigour and intricacies of mathematics and its problems, Oxford Mathematician David Hume discusses his work on networks and expanders.
"A network is a collection of vertices (points) and edges (lines connecting two vertices). They are used to encode everything from transport infrastructure to social media interactions, and from the behaviour of subatomic particles to the structure of a group of symmetries. A common theme throughout these applications, and therefore of interest to civil engineers, advertisers, physicists, and mathematicians (amongst others), is that it is important to know how well connected a given network is. For example, is it possible that two major road closures make it impossible to drive from London to Oxford? An efficient road network should ensure that there are multiple ways to get between any two important places, but we cannot simply tarmac everything! As another example, if as an advertiser, you post adverts on a social media platform, how do you ensure that you reach as many people as possible, without paying to post to every single account?
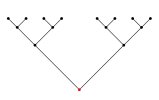
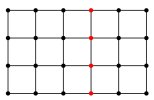
Given a network, we say its cut size is the smallest number of vertices you need to remove, so that the remaining pieces have at most half the original number of vertices in them (in our examples: how many roads need to close before half the population are unable to drive to visit the other half, or how many people need to ignore your advert so that less than half of the users of social media will see it).
Let us say that a family of networks, with increasing numbers of vertices, is called an expander if the cut size of each network is proportional to the number of vertices (1) , and each vertex in a network is the end of at most a fixed number of edges. In theory this would be an optimal solution for a transport network as we can connect as many cities as we need to without needing to work out how to manage the traffic lights at a junction where 5,000 roads all converge. In practice, expanders are as incompatible with the geometry of our world as it is possible for any collection of networks to be.
 (2)
(2)
Expanders, however, are still very interesting and naturally occur in diverse areas: in error-correcting codes in computer science; number theory; and in group theory, where my personal interest lies.
It is, in general very difficult to construct a family of expanders, even though randomly choosing larger and larger networks in which every vertex meets exactly three edges will almost surely produce an expander. The first construction of a family was done by Grigory Margulis - they came from the structure networks of finite groups of symmetries. Other constructions have since been found, most notably a construction of Ramanujan graphs (expanders which, in a particular sense, have the largest possible ratio between their cut-size and their number of vertices), and the fantastically named Zig-Zag product (3) , which builds expanders inductively, starting from two very simple networks.
One question, which seems to have avoided much attention, is the following: how many different expanders are there? To answer this, we first have to deal with the rather sensitive question of what exactly do we mean by different? Does adding one edge change the expander? If so, then the above question is not really very interesting. A more interesting example is provided by Manor Mendel and Assaf Naor: they prove that there are two different expanders so that however you try to associate the vertices in one with the vertices in another, you must either move vertices close that were very far apart before, or else move vertices far apart which previously were very close. In mathematical terms, they are not coarsely equivalent - we cannot even approximately preserve how close vertices are.
In my work, I show that there is a collection of expanders (we can even insist that they are Ramanujan graphs), which is impossible to ennumerate (it is uncountable), such that no pair of them are coarsely equivalent. The technique is to show that for any coarsely equivalent networks, the largest cut size of any network contained in the first with at most n vertices is proportional to the largest cut size of any network contained in the second with at most n vertices. By constructing expanders where these two values are not proportional, we rule out the possibility of such coarse equivalences between them.
The behaviour of cut sizes which is used above to rule out coarse equivalences is of much interest for networks which are not expanders. In my current work I am exploring how cut sizes behave for networks which are 'negatively curved at large scale': this is an area of particular interest in group theory, and plays a key role in the recent proofs of important conjectures in low-dimensional topology: the virtually Haken and virtually fibred conjectures. For such 'negatively curved' groups, cut sizes seem to be related to the dimension of an associated fractal 'at infinity'. With John Mackay and Romain Tessera, we have established this link for an interesting collection of such networks, and are working on developing the technology needed to generalise our results."
(1) This is not the traditional definition, but one of my results proves that a network is an expander in the definition given here if and only it contains an expander in the traditional sense
(2) Two networks with highlighted collections of vertices demonstrating the value of the cut size
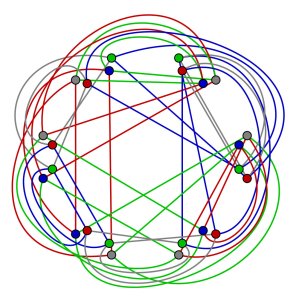
(3) The header image of this article is the Zig-Zag product of a cycle of length 6 with a cycle of length 4