In this collaboration with researchers from the University of Louvain, Renaud Lambiotte from Oxford Mathematics explores the mixing of node attributes in large-scale networks.
A central theme of network science is the heterogeneity present in real-life systems. Take an element, called a node, and its number of connections, called its degree, for instance. Many systems do not have a characteristic degree for the nodes, as they are made of a few highly connected nodes, i.e. hubs, and a majority of poorly connected nodes. Networks are also well-known to be small-world in a majority of contexts, as a few links are typically sufficient to connect any pair of nodes. For instance, the Erdős number of Renaud Lambiotte is 3, as he co-authored a paper with Vincent D. Blondel, who co-authored with Harold S. Shapiro, who co-authored with Paul Erdős. 3 links are sufficient to reach Paul Erdős in the co-authorship network.
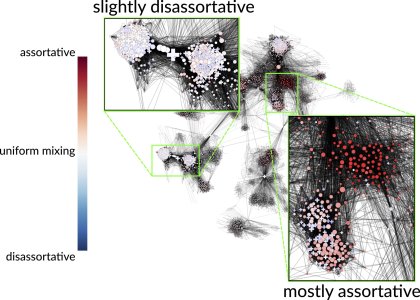
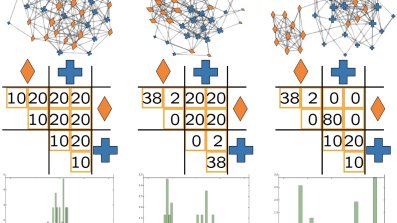
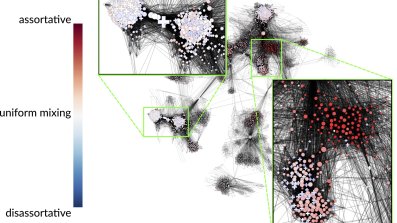
Because of their small-worldness, it is often implicitly assumed that node attributes (for instance, the age or gender of an individual in a social network) are homogeneously mixed in a network and that different regions exhibit the same behaviour. The contribution of this work is to show that this not the case in a variety of systems. Here, the authors focus on assortativity, a network analogue of correlation used to describe how the presence and absence of edges co-varies with the properties of nodes. The authors design a method to characterise the heterogeneity and local variations of assortativity within a network. The left-hand figure (please click to enlarge) for instance, illustrates an analogy to the classical Anscombe’s quartet, with 5 networks having the same number of nodes, number of links and average assortativity, but different local mixing patterns. The method developed by the authors is based on the notion of random walk with restart and allows them to define localized metrics of assortativity in the network. The method is tested on various biological, ecological and social networks, and reveals rich mixing patterns that would be obscured by summarising assortativity with a single statistic. As an example, the right-hand figure shows the local assortativity of gender in a sample of Facebook friendships. One observes that different regions of the graph exhibit strikingly different patterns, confirming that a single variable, e.g. global assortativity, would provide a poor description of the system.
For a more detailed description of the work please click here.