Oxford Mathematician Ricardo Ruiz Baier, in collaboration mainly with the biomedical engineer Alessio Gizzi from Campus Bio-Medico, Rome, have come up with a new class of models that couple diffusion and mechanical stress and which are specifically tailored to the study of cardiac electromechanics.
Cardiac tissue is a complex multiscale medium constituted by highly interconnected units (cardiomyocytes, the cardiac cells) which have remarkable structural and functional properties. Cardiomyocytes are excitable and deformable cells. Inside them, plasma membrane proteins and intracellular organelles all depend on the current mechanical state of the (macroscopic) tissue. Special structures, such as ion channels or gap junctions, rule the passage of charged particles throughout the cell as well as between different cells and their behaviour can be described by reaction-diffusion systems. All these mechanisms work in synchronisation to conform the coordinated contraction and pumping function of the heart.
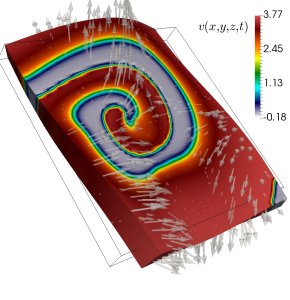
During the cardiac cycle, mechanical deformation undoubtedly affects the electrical impulses that modulate muscle contraction, and also modifies the properties of the substrate where the electrical wave propagates. These multiscale interactions are commonly referred to as the mechano-electric feedback (MEF). Theoretical and clinical studies have been contributing to the systematic investigation of MEF effects for over a century; however, several open questions still remain. For example, and focusing on the cellular level, it is still now not completely understood what is the effective contribution of stretch-activated ion channels and what is the most appropriate way to describe them. In addition, and focusing on the organ scale, the clinical relevance of MEF in patients with heart diseases remains an open issue, specifically in relation to how MEF mechanisms translate into ECGs.
The idea of coupling mechanical stress directly as a mechanism to modify diffusive properties has been exploited for several decades by focusing on the context of dilute solutes in a solid, but remarkable similarities exist between these fundamental processes and the propagation of voltage membrane within cardiac tissue. Indeed, on a macroscopically rigid matrix, the propagating membrane voltage can be regarded as a continuum field undergoing slow diffusion.
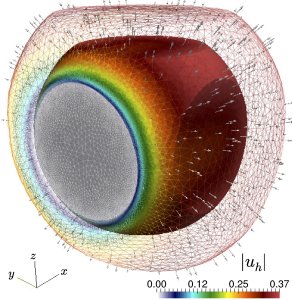
The approach described above basically generalizes Fick's diffusion by using the classical Euler's axioms of continuously distributed matter. An important part of the project, now under development, deals with the stability of the governing partial differential equations, the existence and uniqueness of weak solutions, and the formulation of mixed-primal and fully mixed discretisations needed to compute numerical solutions in an accurate, robust, and efficient manner. Some of the challenges involved relate to strong nonlinearities, heterogeneity, anisotropy, and the very different spatio-temporal scales present in the model. The construction and analysis of the proposed models and methods requires advanced techniques from abstract mathematics, the interpretation of the obtained solutions necessitates a clear understanding of the underlying bio-physical mechanisms, and the implementation (carried out exploiting modern computational architectures) depends on sophisticated tools from computer science.
Other applications of a similar framework are encountered in quite different scenarios, for instance in the modelling of lithium ion batteries. Oxford visiting student Bryan Gomez (from Concepcion, Chile, co-supervised by Ruiz Baier and Gabriel Gatica) is currently looking at the fixed-point solvability and regularity of weak solutions, as well as the construction and analysis of finite element methods tailored for this kind of coupled problems (see also a different perspective focusing on homogenisation and asymptotic analysis, carried out by Oxford Mathematicians Jon Chapman, Alain Goriely, and Colin Please).