Oxford Mathematician Riccardo W. Maffucci is interested in `Nodal lines for eigenfunctions', a multidisciplinary topic in pure mathematics, with application to physics. Its study is at the interface of probability, number theory, analysis, and geometry. The applications to physics include the study of ocean waves, earthquakes, sound and other types of waves. Here he talks about his work.
"Of particular interest to me are the lines that remain stationary during membrane vibrations, the so-called `nodal lines'.

Figure1: Nodal lines
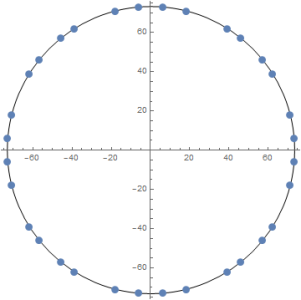
The study of these lines dates back to pioneering experiments by Hooke. The alternative name, `Chladni Plates,' derives from Chladni's work (18th-19th century). One wants to understand the fine geometric properties of the nodal lines. In several cases we introduce a randomisation of the model, to examine events occurring with high probability. The number theory aspects of this problem are related to which numbers are representable as a sum of two squares. For instance one may write 10 = 1+9 but 7 is not the sum of two squares. Their understanding is tantamount to the study of integer coordinate points (`lattice points') on circles.

Figure 2: Lattice points on circles (see larger title image for detail)
The merge of ideas from these disciplines has been brought together by the new and exciting research area of `arithmetic random waves'. There are natural generalisations of these two-dimensional concepts to higher dimensions. For instance in dimension three, one is interested in the `nodal surfaces'.

Figure 3: Nodal Surfaces
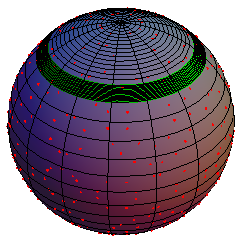
Here the number theory is related to integers expressible as a sum of three squares, and to the lattice points on spheres. For instance, one question concerns the distribution of the lattice points on the surface of the sphere, and in specific regions of it, as in the picture.

Figure 4: Lattice points on spheres
This is a new and exciting field of research with several recent breakthroughs. The group of academics working in this area is growing rapidly. Watch this space."