In many natural systems, such as the climate, the flow of fluids, but also in the motion of certain celestial objects, we observe complicated, irregular, seemingly random behaviours. These are often created by simple deterministic rules, and not by some vast complexity of the system or its inherent randomness. A typical feature of such chaotic systems is the high sensitivity of trajectories to the initial condition, which is also known in popular culture as the butterfly effect. A better understanding of chaos has been the subject of intensive mathematical research for many decades.
The time lags in non-monotone feedback may also cause chaotic behavior, a notable example being the so-called Mackey-Glass equation. This nonlinear delay differential equation was proposed by Canadian scientists Leon Glass and Michael Mackey as a prototype equation for physiological regulatory processes. Variants of this equation have been successfully used to better understand and treat various types of disorders of the hematopoietic system.
The equation has the following form:
\[ \frac{\mathrm{d}}{\mathrm{d}t}x(t)=\beta\frac{x(t-\tau)}{1+x(t-\tau)^n}-\gamma x(t) \]
where all parameters are positive. The apparent simplicity of this model equation is rather deceiving: the Mackey-Glass equation encapsulates incredibly rich mathematical structures embedded into an infinite dimensional phase space, and has provided a lot of work for researchers over the past forty years: to date, more than 4000 papers have cited the original study, yet the emergence of its complex dynamics is not fully understood.
The reason for the presence of the time delay in the model is that following a loss of blood cells, it can take many days before new blood cells can be produced through the activation, differentiation, and proliferation of the appropriate blood stem cells. The unimodal shape of the production term is due to the fact that when the blood cell count is very high, the body does not need more blood cells hence production is low; while when the cell count is low, then your body is in bad shape and hence unable to produce enough. There is an intermediate level when the cell production runs at maximal rate. The interplay of the non-monotone feedback and the time delay makes the behaviour of solutions really tricky.
A specific area of chaos theory research is concerned with the so-called chaos control. Since chaotic behaviour is often undesirable, it is important to understand the ways in which chaos can be avoided. The traditional way of controlling a chaotic system is to pick one of the infinitely many unstable periodic solutions from the chaotic attractor, and add a small perturbation which has the effect of stabilizing this periodic solution. In a recent study, Oxford Mathematician Gergely Röst with Gábor Kiss from Szeged, Hungary, were able to control Mackey-Glass chaos with a completely different approach, which does not require a previous determination of the unstable periodic orbits of the system before the controlling algorithm is designed. The idea is to push all solutions into a domain of the phase space where the feedback is monotone, and keep them there. This way, the long term behaviour is governed by monotone delayed feedback, for which a Poincaré-Bendixson type theorem holds, ensuring that all solutions will converge either to an equilibrium or to a periodic orbit. Hence, chaotic behaviour is excluded. The researchers have shown that several popular control mechanisms can be used to control Mackey-Glass chaos, if the parameters are properly chosen. This way some previously empirically observed controls have been mathematically explained, and also new ways of control have been found such as state dependent delay control.
For more on this topic please click here.
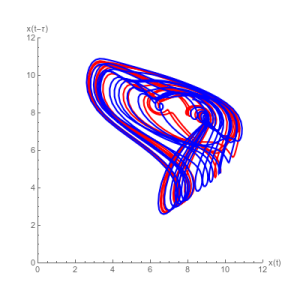
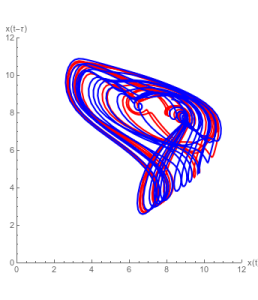
A 2-dimensional projection of the Mackey-Glass attractor
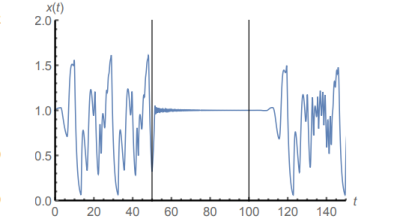
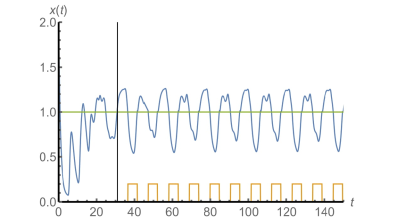
Regulation of a chaotic motion into a periodic one
Control is initiated at t=50, but when it is turned off at t=100, chaotic behaviour returns
Applying a control on short intervals making a complicated solution to behave in a periodic manner.