Oxford Mathematician Mehdi Yazdi talks about his study of tangled ropes in 3-dimensional space.
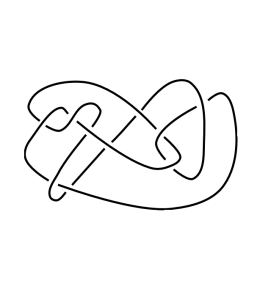
"A 3-manifold is a space that locally looks like the three dimensional space surrounding us. For example, imagine the complement of a closed, possibly tangled rope (i.e., knot) inside 3-dimensional space (Figure 1). One of the essential goals of topology is to understand objects, up to continuous deformations. Therefore, if one can continuously deform one knot into another one, we consider the knots and the corresponding 3-manifolds (i.e., the knot complements) to be the same.
Figure 1
A surface is a two dimensional manifold, meaning that it locally looks like a plane. Examples are a sphere, an American doughnut (i.e., torus, which has one handle) and a pretzel (doughnut with multiple handles!). If we were to remove a small open disk from each of these surfaces, we’d get what we refer to as a surface with boundary. The genus of the surface is the number of handles it has; for example, a doughnut has genus one and a sphere has genus zero.
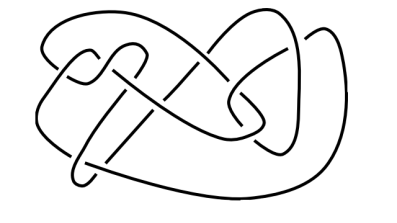
Given two knots that a-priori look totally different, it might be the case that one can be deformed into the other. For example see the knot in Figure 2, which was considered by Ken Miller originally. It is a good exercise to try to untangle this knot (it is possible!). So, a natural question is: how can one tell two knots apart? To answer this question, topologists define invariants for knots. An invariant is a number (or another algebraic object such as a polynomial, a group, etc.) that does not vary under continuous deformations, hence the name. Therefore, if two starting knots have different invariants, they could not be the same, even up to deformations.
Figure 2
A classical and important invariant of a knot is the knot genus. Given any knot, there is an orientable surface in the 3-dimensional space, whose boundary consists of the knot, called a Seifert surface. This is illustrated in Figure 3. This surface is topologically the same as a doughnut with one disk removed from it, even though it looks different! This means that it can be deformed (possibly inside a higher dimensional space) to the standard picture of a doughnut with one disk removed. The genus of the knot K is the minimum genus between all possible orientable surfaces whose boundary is equal to K.
Figure 3
It turns out that determining the genus of a knot is a very difficult question. In fact according to the work of Agol-Hass-Thurston, if we allow both the knot and the ambient manifold to vary, then the question of determining the genus of a knot is NP-complete, roughly meaning that it is as hard as any famous computational problem in computer science. To this date, the only practical way of determining the genus of a knot uses what is called the theory of foliations. The terminology is inspired by the foliations of stratified rocks in geography.
A foliation of a 3-manifold is a decomposition of the 3-manifold into surfaces (called leaves), such that locally, the surfaces fit together like a stack of papers. The caveat is that we allow non-compact surfaces as well. As an example, see the Reeb foliations of the solid torus in Figure 4.
Figure 4
A foliation is called Reeb-less if there is no copy of the foliated solid torus as in Figure 3 anywhere in the 3-manifold. It was Thurston’s discovery that a Seifert surface S for a knot K has the smallest possible genus, if and only if S is a leaf of a Reeb-less foliation of the complement of K. This is only one of many interesting applications of Reeb-less foliations for deducing non-trivial facts about 3-manifolds. Another property being detected by Reeb-less foliations (discovered by Novikov) is whether the manifold has a non-trivial prime decomposition (which we will not define here). Therefore understanding the structure of Reeb-less foliations, and classifying them is of importance.
Kronheimer and Mrowka proved that if we consider foliations up to continuous deformation (of their tangent plane fields), then there are, typically, finitely many Reeb-less foliations on a fixed ambient 3-manifold M. This gives some hope for the classification.
By the work of Pontrjagin and Stiefel, the homotopy classes of plane fields on M are classified by two invariants. One of them is the Euler class of the tangent bundle, which lives in the second cohomology group of M. Our attention will be on the Euler class from now on.
Building on the work of Roussarie, Thurston proved that the evaluation of the Euler class of a Reeb-less foliation on a compact surface cannot exceed the Euler characteristic of the surface in absolute value. In this case,we say that the Euler class has norm at most one. In 1976 Thurston conjectured that a converse should be true when M is hyperbolic (which is a `generic’ condition by Thurston’s work on hyperbolisation of 3-manifolds). That is, every cohomology class of norm one is realised as the Euler class of some Reeb-less foliation on M.
Together with David Gabai, we disproved this conjecture. The main tool is the fully-marked surface theorem, which can have other potential applications. Recall that the evaluation of the Euler class of a Reeb-less foliation on a surface, cannot exceed the complexity of the surface. On the other hand, the equality happens for every compact leaf of the foliation. The fully-marked surface theorem gives a converse to this statement for closed hyperbolic manifolds, up to homotopy of plane fields of Reeb-less foliations."
For more on Mehdi's work together with David Gabai at Princeton University click here.