Free suspended liquid films or sheets are often formed during industrial production of sprays as well as in natural processes such as sea spray. Early experimental and theoretical investigations of them were done by French physicist Felix Savart, who observed liquid sheets forming by a jet impact on a solid surface, or by two jets impacting each other (1833), and British physicist Arthur Mason Worthington, a pioneer in investigation of the crown splash forming after impact of a drop onto a liquid surface. Worthington observed free liquid fims forming in splashes in the form of ejecta sheets (1908).
The industrial production of sprays proceeds typically via the formation of sheets, which break up at the edges to form ribbons. Ribbons are susceptible to the Rayleigh-Plateau instability, and quickly break up into drops. Liquid sheets also happen to puncture far from their boundaries, nucleating a hole or a collection of adjacent holes on the plane of the film. An intriguing example of such hole formation in a crown splash was observed experimentally. Here the whole liquid sheet forming initially the crown breaks up into soap network of filaments.
It is therefore of crucial importance to understand the mechanisms leading to the breakup of sheets. In contrast to jets and liquid threads there is no obvious linear mechanism for sheet breakup. Average thickness of a sheet at breakup start has been measured to lie between 100nm and 100μm, depending on the purity of the liquid, and therefore, van der Waals force cannot play a significant role for breakup formation except perhaps in its very last stages.
Figure 1: This image is a watercolor painting by illustrator Anca Pora following the experimental work of Thoroddsen et al (J. Fluid Mech., 557, 63-72) and provided by Dr. Radu Cimpeanu (Oxford Mathematics).
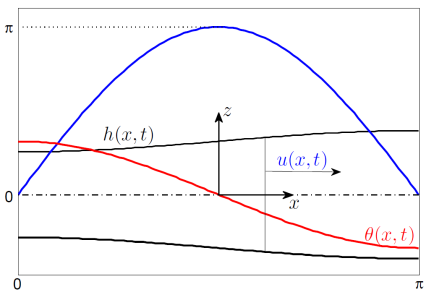
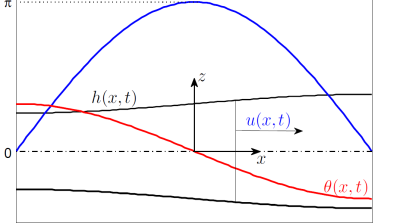
Figure 2: Typical profiles of the height (black), velocity (blue) and temperature (red) for a free liquid sheet
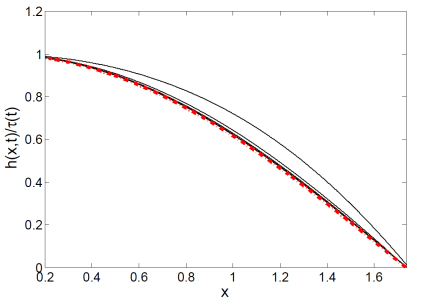
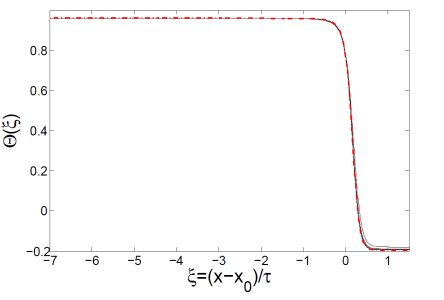
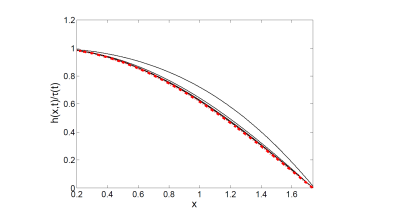
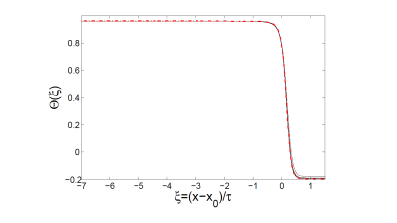
Figure 3: Height profiles in the thinning patch (left) and the sharp forming jump in the temperature (right).
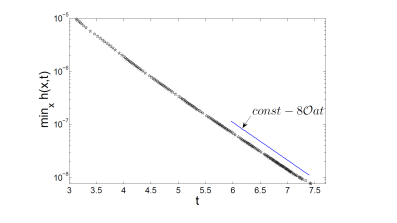
Oxford Mathematician Georgy Kitavtsev together with his collaborators at the University of Bristol and ICMAT, Madrid confirmed recently that variations of temperature or alternatively impurities at the sheet free surfaces (such as diffusing surfactants) promote breakup, because they produce Marangoni forces, which lead to non-steady flows. Intriguingly, even slight variations of temperature or surfactant distribution can lead to formation of sharp gradients of them that promote consequently sheet rupture in an infinite time at an exponential fast rate (see Figs. 3-4). Using matched asymptotic analysis of the underlying nonlinear system of coupled PDEs the researchers were able to derive analytically the corresponding structure of the liquid sheet undergoing rupture. Consistent with the above experimental observations the found solution demonstrates formation of an exponentially thinning patch inside of the sheet and accumulation of the fluid mass into the forming filaments.
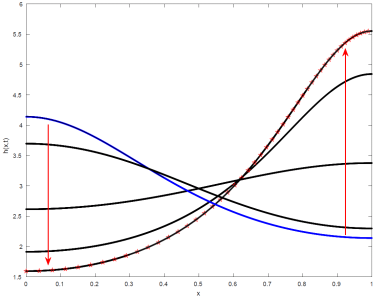
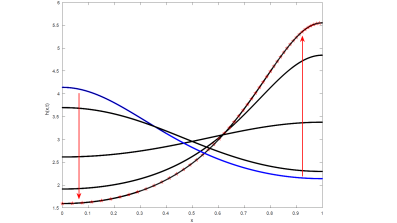
In two subsequent papers the researchers looked now at evolution of pure viscous sheets and showed that generic solutions to a PDE system describing their evolution rather exponentially asymptotically decay to the flat profile. By that they provided a proof of the conjecture formally accepted in the physical literature that a viscous sheet cannot rupture in a finite time in the absence of external forcing. In this proof, a transformation of the PDE system into Lagrangian coordinates turned out to be very useful. Furthermore, in the absence of or for negligible surface tension the Lagrange system is given by a single singular diffusion equation with a source term determined solely by the initial height and velocity distribution in the sheet. In this case, an exponential asymptotic convergence of solutions to the latter equation to the non-homogeneous limit profiles was observed firstly numerically (see Fig. 5) and understood analytically.
Figure 4: Log-linear plot of the minimum height of the sheet as function of time.
Figure 5: Convergence to non-homogeneous stationary height profiles of free viscous liquid sheets in the absence of surface tension.
In summary, these mathematical results open several new perspectives for future industrial applications of free thin liquid sheets and understanding of
their complicated behaviour.