The discomfort experienced when a kidney stone passes through the ureter is often compared to the pain of childbirth. Severe pain can indicate that the stone is too large to naturally dislodge, and surgical intervention may be required. A ureteroscope is inserted into the ureter (passing first through the urethra and the bladder) in a procedure called ureteroscopy. Via a miniscule light and a camera on the scope tip, the patient’s ureter and kidney are viewed by a urologist. The field-of-view is obstructed by blood and stone particles, so a saline solution flows from a bag hanging above the patient, through a long, thin channel (the working channel) that runs through the shaft of the ureteroscope. The fluid flows out of the scope tip, clearing the area in front of the camera and exits the body, flowing in the opposite direction along the outside of the scope through an access sheath, a rigid tube that surrounds the scope. Stones are removed by auxiliary working tools of varying sizes which are introduced through the working channel, providing an undesirable resistance to the flow.
The flow of saline solution is vital for successful ureteroscopy, and understanding and improving this process, known as irrigation, is the subject of this research, carried out by a team comprising Boston Scientific, a medical manufacturing company, Ben Turney, a urologist based at the Nuffield Department of Surgical Sciences in Oxford, and Oxford Mathematicians Sarah Waters, Derek Moulton, and Jessica Williams.
The team apply mathematical modelling techniques to ureteroscope irrigation, based on systematic reductions of the Navier-Stokes equations. Due to the resistance to flow created by working tools, there is a complex relationship between driving pressure, scope geometry, and flow rate properties. The objective has been to understand and exploit that relationship to increase flow for a given driving pressure drop. The team have shown that increased flow and decreased kidney pressures can be accomplished through the use of non-circular cross-sectional shapes for the working channel and the access sheath. These results have led to the filing of a joint patent with Boston Scientific. To complement the reduced analytical models, the team are performing numerical simulations to gain further insight into the flow patterns and resulting pressures within the kidney for a given operating set-up.
Due to the real-world application of this modelling, it is vital that the predictions are validated via experiments. The researchers have performed bench-top flow tests to confirm their analytical models, and particle imaging velocimetry (PIV) to compare against their numerical simulations for the flow within the kidney. This work in constructing a mathematical framework to describe ureteroscope irrigation has significant potential in quantifying irrigation flow and improving scope design.
Images:
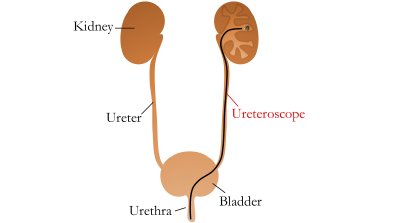
Left: A diagram of the urinary system. The ureteroscope is inserted into the urethra, passing through the bladder, ureter, and into the kidney.
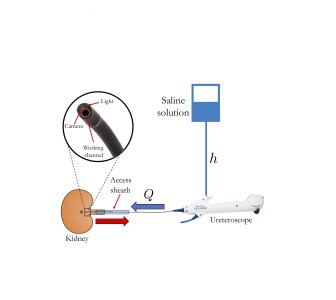
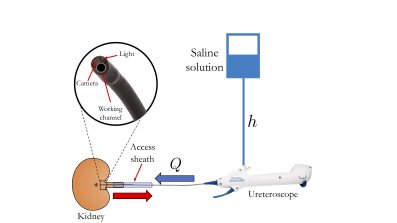
Right: An idealised ureteroscopy set-up. The bag of saline solution is at a height, above the patient. The ureteroscope shaft, containing a working channel, is inserted into the patient. The fluid is driven through the working channel with flow rate by the applied pressure drop, and returns back through an access sheath.
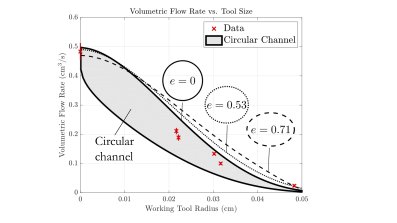
Left: The predicted flow rate through a working channel of circular cross-section containing a working tool of circular cross-section (shaded region). Upper black line of the working tool is at the edge of the channel, the lower line is in the centre. This is compared with experimental data from bench-top experiments (red data points). The dashed and dotted lines are for working channels of elliptical cross-sections with elliptical eccentricity values 0.53 and 0.71. The working tool is in the position that optimises the flow (at the edge of the channel).
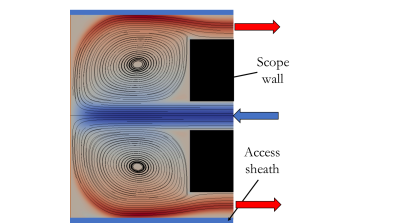
Right: Streamlines for simulated flow exiting the working channel into the kidney and returning back through the access sheath. Computed using open-source finite element library oomph-lib.