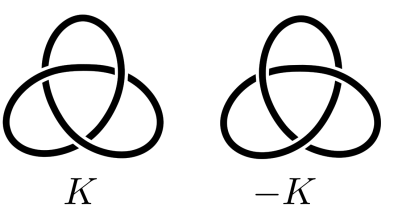Knots are isotopy classes of smooth embeddings of $S^1$ in to $S^3$. Intuitively a knot can be thought of as an elastic closed curve in space, that can be deformed without tearing. Oxford Mathematician Daniele Celoria explains.
"Knots are ubiquitous in the study of the topological and geometrical properties of manifolds with dimension $3$ and $4$. This is due to the fact that they can be used to prescribe the attachment instructions for the "building blocks" of these spaces, through a process known as surgery.
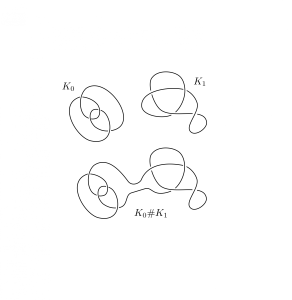
Figure 1. The connected sum of two knots. Strictly speaking this operation is defined only for oriented knots, but this distinction is irrelevant in the following.
There is a well defined notion of addition for two knots, called connected sum and denoted by $\#$, described in Figure3. However, the resulting algebraic structure is quite uninteresting. Namely, the set of knots with the operation $\#$ is just an infinitely generated monoid.
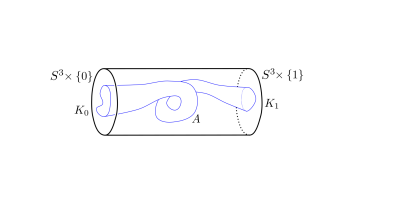
If instead we consider a coarser equivalence relation on the set of embeddings $S^1 \hookrightarrow S^3$, we obtain a group called the smooth concordance group $\mathcal{C}$. Two knots are said to be concordant if there exists a smooth and properly embedded annulus $A \cong S^1 \times [0,1]$ in the product $S^3 \times [0,1]$ interpolating between the knots, as schematically shown in Figure 3.
Figure 2. A schematic picture for a properly embedded annulus connecting two knots in $S^3 \times [0,1]$.
Knots representing the identity in $\mathcal{C}$ are those bounding a properly embedded disc in the 4-ball. The inverse of the class represented by a knot $K$ is given by the class containing its mirror $-K$, which is just the reflection of $K$ (see Figure 3).
It is possible to define the equivalence relation of concordance for knots in a 3-manifold $Y$ other than the 3-sphere; we denote the resulting set by $\mathcal{C}_Y$. Note that $\mathcal{C}_Y$ can not be a group, since connected sums do not preserve the ambient 3-manifold. It is easy to realise that $\mathcal{C}_Y$ splits along free homotopy classes of loops in $Y$.
Figure 3. A knot and its mirror. It can be obtained by taking any diagram of $K$, and switching all crossings.
There is a well-defined and splitting-preserving action of $\mathcal{C}$ (so concordance classes of knots in the 3-sphere) on $\mathcal{C}_Y$, induced by connected sum with a local (i.e. contained in a 3-ball) knot. An equivalence class of concordances up to this action is called an almost-concordance class.
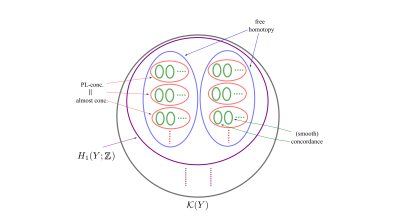
So we can partition the set $\mathcal{K}(Y)$ of knots in a $3$-manifold $Y$ into (first) homology, free homotopy, almost-concordance and smooth concordance classes, as described in Figure 4.
Figure 4. Nested partitions of $\mathcal{K}(Y)$. Click to enlarge.
In my paper I defined an invariant of almost-concordance extracted from knot Floer homology, and proved that all 3-manifolds with non-abelian fundamental group and most lens spaces admit infinitely many non almost-concordant classes. Moreover each element in all of these classes represents the trivial first homology class in its ambient $3$-manifold. This result has been subsequently generalised to all 3-manifolds by Friedl-Nagel-Orson-Powell."