Oxford Mathematician Yinan Wang talks about his and colleagues' work on classification of elliptic Calabi-Yau manifolds and geometric solutions of F-theory.
"In the past century, the unification of gravitational force and particle physics was the ultimate dream for many theoretical physicists. String theory is currently the most well-established example of such a grand unification theory. In the past decades, research in this field has produced many fruitful applications in quantum field theory, condensed matter physics, quantum information theory and pure mathematics.
Nonetheless, the string theory framework is complicated since there are many different versions of string theory: I, IIA, IIB, heterotic, M-theory. Moreover, string theory lives in a very high dimensional spacetime: 10 or 11 dimensions including the time direction. To get a description of our real world four-dimensional physics, we need to put this higher dimensional theory on a very small space (this procedure is called "compactification''). There could be a zillion of such geometric spaces, and their total number was completely unknown.
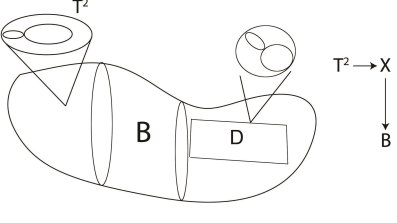
In our recent work, we studied the compactification of F-theory, which is a geometric description of IIB string theory. This framework unifies the M-theory solutions in many cases as well. In particular, the geometric spaces in this approach are elliptic Calabi-Yau manifolds. They can be thought as having an additional torus over each point on a "base'' space.
Figure 1: A picture of elliptic Calabi-Yau manifold
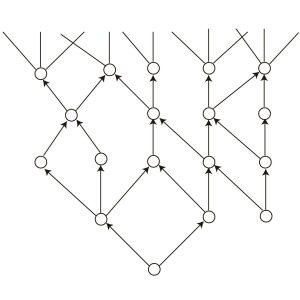
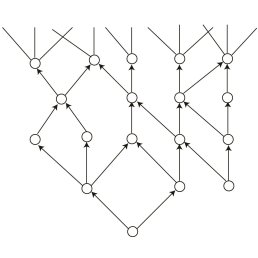
We partially classified the sets of four-dimensional and six-dimensional bases. They equivalently have two or three complex dimensions if one describes them using complex numbers. In particular, we probed the huge connected network of complex 3D bases, which was estimated to contain more than $10^{3,000}$ nodes. The F-theory compactification on an elliptic Calabi-Yau manifold over such bases will give rise to different 4D physics. Interestingly, we found that the 4D physical model on a typical geometric space is quite different from our known particle physics. The gauge groups in the F-theory models are usually $SU(2)$, $F_4$, $G_2$ and $E_8$ in term of Lie algebra classification, while our real world particle physics has $SU(3)\times SU(2)\times U(1)$ gauge group. Moreover, there are a number of mysterious "strongly coupled'' sectors in a typical F-theory model, without any known gauge theory description. There are many things to be explored about these strongly coupled sectors in the future, which requires novel quantum field theory and geometric techniques. Finally, we hope to figure out whether our particle physics standard model can be realized on such a typical F-theory construction."
Figure 2: A part of the network of complex 3D base geometries
For more on the probing of networks click here
For the work on strongly coupled sector of a typical F-theory model click here