Oxford Mathematicians Anna Seigal, Heather Harrington, Mariano Beguerisse Diaz and colleagues talk about their work on trying to find cancer cell lines with similar responses by clustering them with structural constraints.
"Modern data analysis centres around the comparison of multiple different changing factors or variables. For example, we want to understand how different cells respond to different experimental conditions, under a range of doses, and for various different output measurements, across different timepoints. The structure in such data sets guide the design of new drugs in personalized medicine.
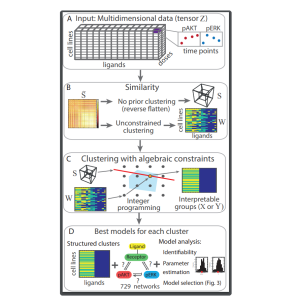
A key way to find structure in data is by clustering: partitioning the data into subsets within which the data share some similarity. As multi-dimensional data sets become more prevalent, the question of how to cluster them becomes more important. Usual clustering algorithms can be used, but they do not conserve the multi-dimensional structure of the original data, and this flattens the insights that can be made, and hampers the interpretability of the results.
In our paper, we introduce a method to cluster multi-dimensional data while respecting constraints on the composition of each cluster, designed to attribute differences between clusters to interpretable differences for the application at hand. In our method, a high similarity is not enough to cluster two data points together. We also require that their similarity is compatible with a shared explanation. We do this by placing algebraic constraints on the shapes of the clusters. This method allows for better control of spurious associations in the data than other approaches, by constraining the associations to only retain those with a consistent basis for similarity.
We apply our method on an extensive experimental dataset detailing the temporal phosphorylation response of signaling molecules in genetically diverse breast cancer cell lines in response to different ligands (or experimental conditions). In this setting, we aim to find sets of experiments whose responses are similar, and to interpret these similarities in terms of the unknown underlying signaling mechanisms. In our data set each experiment is given by a cell line and a ligand. One example of a mechanistic interpretation we could make from a similarity is that the cell lines in a cluster share a mutation, and the ligands are those whose effect is altered by the mutation.
We constrain the clusters to be rectangular, i.e. to match a subset of cell lines with a subset of ligands. The constraints only keep experimental measurements that are compatible with a mechanistic interpretation. This facilitates biological insights to be gleaned from the clusters obtained. In our paper, we present two variations of the algorithm:
1. The method can be applied directly to a dataset (i.e. as a standalone clustering tool). Similarities between data points are encoded in a similarity tensor, the higher-dimensional analogue of a similarity matrix, and constraints about which clusters are allowed form the equations and inequalities in the entries of an unknown tensor, which encodes the clustering assignment.
2. The method can be applied in combination with other clustering methods, to impose constraints onto pre-existing clusters. The distance between partitions is given by the number of experiments whose clustering assignment changes. Hence this method can be used in conjunction with any other state-of-the-art method and preserve the features of an initial clustering that are compatible with the constraints.
In both implementations, the interpretability constraints can be encoded as algebraic inequalities in the entries of the clustering assignment, which gives an integer linear program. This can be solved to optimality, using the branch-and-bound algorithm, to find the best clustering assignment.
Any other constraints that give linear inequalities can also be used. There are possibilities to apply the methodology to problems with other constraints, such as restricting on the size of cluster, imposing certain combinations of data, or finding communities in networks with quotas."