Oxford Mathematician Ric Wade explains how right-angled Artin groups, once neglected, are now central figures in low-dimension topology.
"Right-angled Artin groups (colloquially known as a RAAGs or 'rags') form a family of finitely presented discrete groups that generalise free-abelian groups (where all the generators commute) and free groups (where no generators commute). Every finite graph $\Gamma$ defines a finitely presented group $A_\Gamma$ generated by the vertex set, with the restriction that $vw=wv$ if two vertices $v$ and $w$ are connected by an edge (in other words, adjacent vertices commute). If the graph is complete (so that any two vertices are connected by an edge) then $A_\Gamma$ is a free-abelian group, and if the graph $\Gamma$ has no edges, then $A_\Gamma$ is a free group. Loops and multiple edges between vertices do not affect the group that we get using this construction, so in graph-theoretic language we can assume that $\Gamma$ is simple.
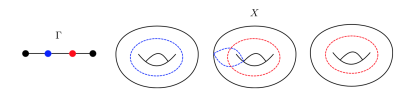
Figure 1: A graph $\Gamma$ and a topological space $X$ such that $\pi_1(X)=A_\Gamma$.
One example is given by the graph $\Gamma$ which consists of three edges joined in a line. In this case, the group $A_\Gamma$ that we get is obtained by taking the fundamental group of three tori, where the middle tours has its meridian and equator glued to the equators of the other two tori (see Figure 1).
Possibly because the definition of these groups sounds quite contrived, right-angled Artin groups saw relatively little interest until the 21st century. However, they have become central figures in recent progress in low-dimension topology. I can highlight two reasons for this:
- RAAGs have a nice simple combinatorial description, which is helpful for proving group-theoretic results.
- RAAGs have a surprisingly diverse subgroup structure, which means that many groups that are harder to understand can be embedded in these 'simpler' groups.
The flagship result with respect to this viewpoint is a theorem of Agol (building upon work of Wise, Kahn-Markovic, Sageev, and others), which states that the fundamental group of every closed hyperbolic 3-manifold has a finite index subgroup which embeds into a right-angled Artin group in a particularly nice way. This was a key step in the resolution of Thurston's virtual fibering conjecture, which was one of the major open problems in the area not to fall to Perelman's solution of the Poincare conjecture.
I'm interested in automorphism groups of right-angled Artin groups: the groups of their self-symmetries. Going back to thinking about RAAGs interpolating between free and free-abelian groups, these automorphism groups should have behaviour similar to $GL(n,\mathbb{Z})=Aut(\mathbb{Z}^n)$ from the free-abelian side, and automorphism groups of free groups on the free side. In practice, such interpolation results are much harder to obtain. In recent work with Matthew Day at the University of Arkansas, we have been studying the finiteness properties of these automorphism groups. Roughly speaking, this is the search for nice topological spaces (specifically, classifying spaces) that describe $Aut(A_\Gamma)$ for an arbitrary RAAG. For $GL(n,\mathbb{Z})$ the construction of such spaces goes back to work of Borel and Serre, who used deformation spaces of tori to build classifying spaces of certain finite index subgroups of $GL(n,\mathbb{Z})$ known as congruence subgroups. A classifying space for a finite-index subgroup of $Aut(F_n)$ was built by Culler and Vogtmann, using a deformation space of metric graphs (these appear as tropical curves in the world of tropical geometry). In a paper due to appear in the Journal of Topology, we prove the following theorem:
Theorem 1 (Day-W). For any graph $\Gamma$, the group $Aut(A_\Gamma)$ has a finite-index subgroup with a classifying space given by a finite cell complex.
Our classifying space is built by carefully splicing together deformation spaces of tori, deformation spaces of graphs, and classifying spaces for right-angled Artin groups called Salvetti complexes. This theorem gives restrictions on the algebraic invariants of $Aut(A_\Gamma)$; in particular it says that the cohomology ring $H^*(Aut(A_\Gamma);\mathbb{Q})$ is finitely generated as a $\mathbb{Q}$-vector space. Our construction is inductive rather than completely concrete, however the construction does allow for some calculations (via spectral sequence arguments, for instance). The next step for us in this programme is to give an algorithm to find the virtual cohomological dimension of any automorphism group $Aut(A_\Gamma)$, and we hope that other problems involving these automorphism groups can be understood through these classifying spaces as well."