Oxford Mathematician Ebrahim Patel talks about his work using max-plus algebra to improve airport scheduling and to define optimal railway networks.
"Typically arising from scheduling problems, max-plus algebra (MPA) offers an elegant way to understand the behaviour of a complex system depicted as a network of nodes. For example, an arrow points from node a to node b if b is dependent on a. Thus, I used MPA to better schedule Dubai's airport activities as part of the Oxford-Emirates Data Science Lab. The task was to model the dependence on activities such as cleaning and passenger boarding times to ultimately reduce delays and their impact.
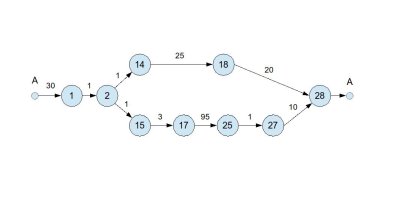
Fig 1 shows a network of some such activities that need to take place before the departure of a plane. For example, activity 28 (departure) is dependent on the completion of activities 18 and 27, taking 20 and 10 minutes respectively. Additionally, at least 30 minutes must elapse before this network of activities is repeated, which represents the preparation of a subsequent departure at the same gate. Scheduling is thus made periodic by connecting the last activity, 28, to activity 1, indicated by connecting node A.
Figure 1: Network of activities prior to a plane departure
Suppose that we know $x_{28}(k)$, the $k^\text{th}$ departure time at this gate. Then the earliest time (in minutes) that this set of activities can start again for the next departure is $$ x_1(k+1) = x_{28}(k) + 30 \ .$$ The start times of all other activities are obtained similarly. In particular, for activities like 28, that depend on more than one activity, we have $$ x_{28}(k) = \max\{ x_{18}(k) + 20, x_{27}(k)+10 \} \ .$$ Overall, we obtain a system of equations, which has a natural interpretation in MPA. The eigenvalues of the max-plus system correspond to the turnaround time of the network; here, we obtain turnaround time $= 141$ minutes, which can also be found by employing critical path analysis. However, MPA gives a deterministic, linear algebraic handle on this process, and it can also deal with a more complicated network of activities, where the period of the activity times is larger than one. How is it linear? Via the simple operator transformations: $\max \longmapsto \oplus $ and $+ \longmapsto \otimes $. The operators $\oplus$ and $\otimes$ play the same role in MPA as $+$ and $\times$ do in conventional mathematics (this is easy to check!).
The work with Emirates ended before being implemented. But it was another transport application that inspired this model. In the railway network, we can think of nodes as stations and edges as tracks. By imposing the rule that trains at each station must only depart once trains have arrived from other stations, a max-plus equation is formed since the earliest departure time of a train is the maximum of the times of arriving trains. Whilst this might seem constraining, it is in fact a standard starting point for efficient mathematical modelling. The beauty of MPA is the intimate link between the mathematics and network theory: one only needs a standard understanding of the mathematics, following which problems can often be solved by straightforward optimisation of network structures.
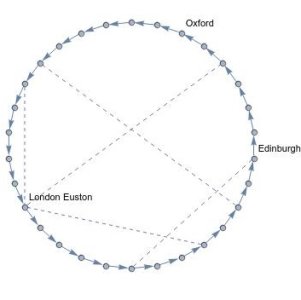
Indeed, by supervising Masters level projects in this area, most recently for the Oxford MMSC course, a big question that has been addressed is, 'what is the optimal railway network?' Starting with an abstraction of the railway network, then strategically adding nodes and edges, it turns out that a one-way ring layout is best! Whilst this allows stations to wait only for one train before departures, it obviously looks impractical; for instance, to travel from London Euston to Oxford, it seems one would have to go through Edinburgh! But actually the additional nodes in this layout represent platforms within stations, and the dashed edges represent walks between these platforms. This is what produces the impracticality illusion; we have in fact split London Euston into multiple substations, i.e., platforms. So MPA allows a lot of room for manoeuvre to produce optimal railway networks. This work has also thrown up a multitude of interesting theoretical questions, such as the concepts of eigenvalues and eigenvectors in generalised models; so this is a classic example of a two-way benefit: pure mathematics feeds applied mathematics, which feeds back to pure.
Figure 2: The optimal railway network is a one-way ring?
In my latest work, I am developing an extension of MPA called Maxmin-$\omega$, which has provided novel areas of application. Here, we obtain a solely max-plus system when $\omega=1$ and a solely min-plus system when $\omega=0$ (where nodal activities are started upon receipt of the first instead of the last input, as in MPA). When ${\omega\in(0,1)}$, the system is governed by a combination of max- and min-plus algebra. The parameter $\omega$ therefore behaves as a threshold, and this yields a deterministic way of thinking about threshold models of information proliferation. I particularly want to apply this to periodic information diffusion data, such as retweet activity on Twitter and neural networks, which are constantly bouncing signals amongst neurons. The work will be presented at Sunbelt, the biggest social networks conference, this summer, to be held in Montreal. In keeping with the nature of this modern data-centric age, the possibilities for MPA and its extensions are exciting."
For more on Ebrahim's research click here.