Minimal Lagrangians are key objects in geometry, with many connections ranging from classical problems through to modern theoretical physics, but where and how do we find them? Oxford Mathematician Jason Lotay describes some of his research on these questions.
"A classical problem in geometry going back at least to Ancient Greece is the so-called isoperimetric problem: what is the shortest curve in the plane enclosing a given area A? The answer is a circle:


Variants of this problem for curves include finding the shortest curve representing a given class of loops. For example on a torus, we see that both the blue and red curves on the right are shortest curves which represent the original blue loop on the left.


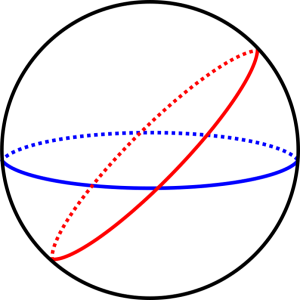
If we look at a sphere, however, then there is no shortest curve representing any given loop, since we can contract every curve to a point. A natural question on a sphere is to ask for the shortest curve dividing the sphere into regions of equal area, which sounds more like the original isoperimetric problem. The answer is (any) equator:


The answer for the shortest curve in every case we have considered has in fact been a minimal Lagrangian: on surfaces, minimal Lagrangians are just geodesics, which are curves that are critical for length. Moreover, deformations of curves in the plane which contain the same enclosed area, or of the curves on the sphere which always divide the sphere into regions of equal area, are known as Hamiltonian isotopies. In particular, we can rephrase the problem we considered on the sphere as finding minimal Lagrangians in the Hamiltonian isotopy class of the original blue curve on the left sphere.
These ideas generalize to higher dimensions: we replace the surface by a particular type of even-dimensional space known as a Kähler-Einstein manifold M, we replace curves by Lagrangians that are certain geometric objects in M which are half the dimension of M (just like curves are 1-dimensional whilst surfaces are 2-dimensional), and Hamiltonian isotopies are special types of deformations we allow of a given Lagrangian that generalize the area preserving deformations we had before. Then minimal Lagrangians are just Lagrangians which are critical for volume, just as geodesics were curves which are critical for length, so we can think of them a bit like soap films:


Kähler-Einstein manifolds and minimal Lagrangians form an important part of modern geometry, particularly since they include so-called Calabi-Yau manifolds and special Lagrangians, which play a key role in the study of Mirror Symmetry and in String Theory in theoretical physics. The definition of Kähler-Einstein manifolds depends on a constant, which can be positive, zero (which is the Calabi-Yau setting) or negative, and the behaviour of these spaces and the minimal Lagrangians in them is quite different in each case.
The positive Kähler-Einstein manifolds include complex projective spaces, which generalize the sphere, and here minimal Lagrangians are typically easy to find because the ambient space has a lot of symmetries (like the sphere). An interesting question therefore is: which minimal Lagrangian in a positive Kähler-Einstein manifold has the least volume in its Hamiltonian isotopy class? For the sphere and curves which divide the sphere into two regions of equal area, the answer is the equator. There is a well-known and unsolved conjecture, due to Oh, that says for complex projective spaces there is a natural minimal Lagrangian (called the Clifford torus) which is volume-minimizing under Hamiltonian isotopies: this is the higher-dimensional analogue of our isoperimetric problem on the sphere.
A natural way to try to solve Oh’s conjecture is to start with a Lagrangian which is related to the Clifford torus by a Hamiltonian isotopy and then deform the Lagrangian by minimizing volume as quickly as possible: this is called Lagrangian mean curvature flow. I have studied Lagrangian mean curvature flow extensively, most recently with my collaborators Ben Lambert (Oxford) and Felix Schulze (UCL), with a hope to try to tackle this and other related problems.
In particular, in the Calabi-Yau setting (which is, in some sense, the analogue of the flat plane or the torus), Lagrangian mean curvature flow is particularly appealing and there is a conjecture due to Thomas and Yau that predicts the behaviour of the flow in special cases. I am actively studying approaches to this conjecture, which would hopefully pave the way towards understanding how we can potentially “break up” a Lagrangian into special Lagrangian pieces, in the same way that we now know how to break up 3-dimensional spaces into special (or “prime”) pieces using the geometric flow known as the Ricci flow.
Finally, in negative Kähler-Einstein manifolds (which are the higher-dimensional analogues of surfaces with more 'holes' than the torus), minimal Lagrangians are typically very hard to find. In fact, they are conjectured to be unique in their Hamiltonian isotopy class. This is obviously false for positive Kähler-Einstein manifolds since, for example, on the sphere we can rotate the sphere to get the red geodesic starting from the blue one, which is a Hamiltonian isotopy.

That said, there are many examples of negative Kähler-Einstein manifolds, so it is natural to ask whether they contain minimal Lagrangians or not. Together with my collaborator Tommaso Pacini (Turin), I recently addressed this question by finding infinitely many new cases of negative Kähler-Einstein manifolds containing minimal Lagrangians.
Although we have made a lot of progress in understanding minimal Lagrangians, there are many fascinating and challenging problems left to study. Minimal Lagrangians certainly are fantastic beasts and we should try our best to find them!"
For more on Jason's work:
Ancient solutions in Lagrangian mean curvature flow
Remarks on the self-shrinking Clifford torus
From minimal Lagrangian to J-minimal submanifolds: persistence and uniqueness