Elementary particles in two dimensional systems are not constrained by the fermion-boson alternative. They are so-called "anyons''. Anyon systems are modelled by modular tensor categories, and form an active area of research. Oxford Mathematician André Henriques explains his interest in the question.
"In the standard model of quantum physics, which describes our world at subatomic scales, the elementary particles are divided into two kinds. The fermions on the one hand form the matter that is present all around us (examples include electrons, quarks, neutrinos, etc.). And the bosons are responsible for the transmission of the four fundamental forces (e.g. photons, gluons, the Higgs boson, etc.).
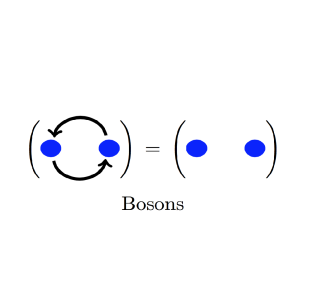
Mathematically, one can devise alternative universes with different laws of physics, in which the number of elementary particles is different from that of our physical world. But the fundamental dichotomy between bosons and fermions is dictated by the $3$-dimensionality of the space we live in. Fermions are defined by the property that, under exchanging two particles of the same kind, the wave-function of the many body system acquires a minus sign, while for bosons, that same operation leave the wave-function unchanged.

The number which appears above is constrained to be $\pm1$ because, in $3$ dimensions, the operation of twice exchanging two particles is homotopic to the operation of doing nothing. That is, there exists a one-parameter family of operations where, at one end of the family you have the operation of twice exchanging the particles, and at the other end of the family you have the operation of doing nothing:
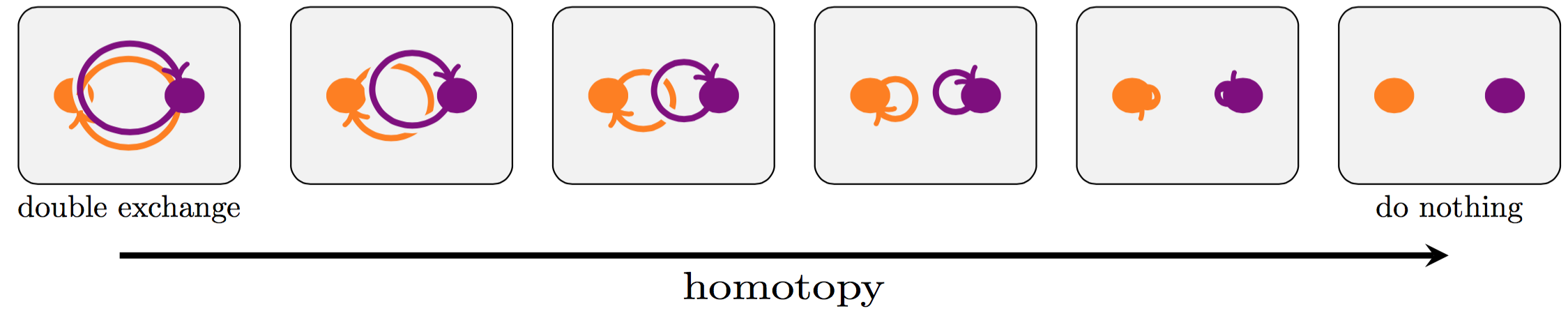
The existence of that homotopy forces the above number to square to 1, which leaves us only +1 or -1 as possible values.
Let us now switch to flatland, in which space is 2-dimensional. The operations drawn in the above pictures are no longer homotopic, and the elementary excitations (quasi-particles) are no longer constrained to the Fermi-Bose alternative. They can be anything interpolating between fermions and bosons, and have thus been called "anyons''. The typical approach to mathematically formalise the notion of anyon systems is that of modular tensor categories. The objects of the modular tensor category represent the different species of anyons, and the tensor product of the object in the modular tensor category corresponds to the operation of letting two (or more) anyons collide into each other.
The construction of modular tensor categories is a generally difficult task, and every time one finds a new source of examples, this is treated as a nice result. An important class of examples come from the so-called quantum groups. These are certain Hopf algebras closely related to the classical Lie groups (e.g. the group of orthogonal rotations of $n$-dimensional space). The modular tensor categories coming from quantum groups have a very nice structure: their set of simple objects (= anyon types) are in bijection with the lattice points inside a simplex.

The simplest but already quite interesting example of a modular tensor category is known as the Fibonacci modular tensor category. It has a single non-trivial anyon type. The latter has the property that, by letting n identical anyons collide, the number of possible quantum states of the output is exactly equal to the n-th Fibonacci number. Finding new examples of modular tensor categories is an active field of research, and there exists an important conjecture which states that every modular tensor category is related, in a specific way, to quantum groups.
In my study of the representation theory of certain infinite dimensional groups, I have found a new construction of the quantum group modular tensor categories. They are constructed as centres of categories of representations of the based loop group. In the future, I hope to apply based loop group techniques to other structures in 2-dimensional physics, such as boundary conditions, and line defects."