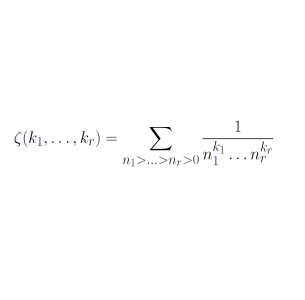Oxford Mathematician Nils Matthes talks about trying to understand old numbers using new techniques.
"The Riemann zeta function is arguably one of the most important objects in arithmetic. It encodes deep information about the whole numbers; for example the celebrated Riemann hypothesis, which gives a precise location of its zeros, predicts deep information about the prime numbers. In my research, I am mostly interested in the special values of the Riemann zeta function at integers $k\geq 2$,
$(1)\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\displaystyle\zeta(k)=\sum_{n=1}^{\infty}\frac{1}{n^k}, \qquad$
called zeta values. Their appearance is by no means confined to arithmetic and they are known to appear in a multitude of other mathematical areas (hyperbolic geometry, algebraic K-theory, knot theory, ...) and even in amplitude computations in high energy physics. A better understanding of these numbers therefore has potentially important consequences for other fields as well.
One of the earliest results in this direction is due to Euler, who showed in 1734 that for even values of $k$ the zeta value $\zeta(k)$ is an explicit rational multiple of $\pi^k$. Therefore, the even zeta values satisfy a rather simple algebraic relation; up to a rational factor they are all powers of $\zeta(2)$. On the other hand, Euler was unable to show the analogous result for odd zeta values and moreover did not find any algebraic relations between $\pi$ and the $\zeta(2k-1)$. It is nowadays widely believed that $\zeta(2k-1)$ cannot be written as a rational multiple of $\pi^{2k-1}$ and that in fact no such algebraic relations exist.
In the 1920s, a new point of view on the odd zeta values emerged from work of Ramanujan who was able to express the difference between $\zeta(2k-1)$ and a certain rational multiple of $\pi^{2k-1}$ as a Lambert series. For example, in the case of $\zeta(3)$, his formula reads
$\displaystyle(2)\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\frac{7\pi^3}{180}-\zeta(3)=2\sum_{n=1}^{\infty}\frac{1}{n^3(e^{2\pi n}-1)}. $
As it turns out, Ramanujan's formula is much better suited for numerical computation of the odd zeta values than (1). Indeed, the first $10$ terms on the right hand side of (2) are already sufficient to compute the decimal expansion of $\zeta(3)$ correctly up to $30$ digits. This is because the series in (2) converges exponentially quickly while the series in (1) has a much slower rate of convergence.
Somewhat later, it was realised that Ramanujan essentially discovered that $\zeta(2k-1)$ is a period integral of the Eisenstein series $G_{2k}$. These are particularly simple examples of modular forms, a certain class of holomorphic functions on the complex upper half-plane which transform in a rather simple way under Möbius transformations. Modular forms are ubiquitous in modern number theory; for example, they play a key role in Andrew Wiles' proof of Fermat's last theorem. Moreover, since the even zeta value $\zeta(2k)$ appears as the constant term of the Fourier expansion of $G_{2k}$, all zeta values naturally arise from Eisenstein series.
In the course of his studies, Euler also introduced multiple zeta values \begin{equation} \zeta(k_1,\ldots,k_r)=\sum_{n_1>\ldots>n_r>0}\frac{1}{n_1^{k_1}\ldots n_r^{k_r}}, \quad \mbox{for } k_1,\ldots,k_r \geq 1, \, k_1 \geq 2, \end{equation} which generalize (1) to several arguments. Again, these numbers appear in a variety of mathematical contexts and a basic problem is to understand their algebraic relations completely. It turns out that multiple zeta values are also related to modular forms but that here the relationship is much more mysterious. It was uncovered only in 2006 by Herbert Gangl, Masanobu Kaneko and Don Zagier who found the following relation among double zeta values: \begin{equation} \label{eqn:GKZ} 28\zeta(9,3)+150\zeta(7,5)+168\zeta(5,7)=\frac{5197}{691}\zeta(12). \end{equation} Moreover, they interpreted the coefficients $28,150$ and $168$ on the left hand side in terms of period integrals of a certain modular form of weight $12$. More generally, to every modular form for $\operatorname{PSL}_2(\mathbb Z)$ they associated a $\mathbb Q$-linear relation among certain $\zeta(r,s)$ whose coefficients can again be interpreted using period integrals of modular forms. Their observation is subsumed in the far-reaching Broadhurst-Kreimer conjecture which describes the algebraic structure of multiple zeta values entirely in terms of modular forms.
In light of the seemingly mysterious relationship between multiple zeta values and period integrals of modular forms, it is natural to ask for a common framework accommodating both objects. In my PhD thesis at University of Hamburg, building on foundational work of Francis Brown, Andrey Levin and Benjamin Enriquez, I studied elliptic multiple zeta values which bridge these two seemingly very different worlds. More precisely, elliptic multiple zeta values are holomorphic functions on the upper half plane which on one hand satisfy a first-order differential equation involving Eisenstein series and, on the other, degenerate to multiple zeta values at the cusp $i\infty$. It turns out that some of the rather surprising modular phenomena occurring in the study of multiple zeta values such as the relations found by Gangl-Kaneko-Zagier have more transparent analogues in the elliptic setting, which helps with elucidating the algebraic structure of multiple zeta values. In particular, the study of elliptic multiple zeta values should offer a more conceptual explanation of the Broadhurst-Kreimer conjecture.
To conclude, it should be mentioned that the Riemann zeta function is only the simplest example of a so-called Hasse-Weil L-function. More generally, to any algebraic variety over a number field, one can attach such an L-function which encapsulates deep arithmetic-geometric information in a single analytic object. On the other hand, multiple zeta values are only very special examples of periods in the sense of Maxim Kontsevich and Don Zagier which are defined as the values of certain algebraic integrals. Important and far-reaching conjectures due to Pierre Deligne and Alexander Beilinson predict that the special values of Hasse-Weil L-functions are periods. In the case of L-functions associated with elliptic curves, their conjectures are closely related to the Birch and Swinnerton-Dyer conjecture. In this context, the putative relationship between multiple zeta values and modular forms is part of a much more general program of Francis Brown's which, among other things, aims at expressing periods in the sense of Kontsevich-Zagier as (iterated) integrals of modular forms, with the hope of gaining new insights into both objects."