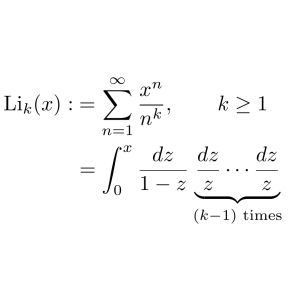Oxford Mathematician Ma Luo talks about his work on constructing iterated integrals, which generalizes usual integrals, to study elliptic and modular curves.
Usual integrals
Given a path $\gamma$ and a differential 1-form $\omega$ on a space $M$, we can parametrize the path $$\gamma:[0,1]\to M, \qquad t\mapsto\gamma(t)$$ and write $\omega$ as $f(t)dt$, then define the usual integral $$\int_\gamma \omega=\int_0^1 f(t)dt.$$ If we have two loops $\alpha$ and $\beta$ based at the same point $x$ on $M$, then $$\int_{\alpha\beta}\omega=\int_\alpha \omega+\int_\beta \omega=\int_{\beta\alpha} \omega.$$ The order of the loops from which we integrate does not affect the result. Therefore, the usual integral can only detect commutative, i.e. abelian, information in the fundamental group $\pi_1(M,x)$.
Iterated integrals
Kuo-Tsai Chen has discovered a generalization of the usual integral as follows: Given a path $\gamma$ and differential 1-forms $\omega_1,\cdots,\omega_r$ on $M$. Write each $\omega_j$ as $f_j(t)dt$ on the parametrized path $\gamma(t)$. Define an iterated integral by \begin{equation}\label{def} \int_\gamma \omega_1\cdots\omega_r=\idotsint\limits_{0\le t_1\le \cdots \le t_r\le 1} f_1(t_1)f_2(t_2)\cdots f_r(t_r) dt_1\cdots dt_r. \end{equation} It is a time ordered integral. Now for the two loops $\alpha$ and $\beta$, we have $$\int_{\alpha\beta}\omega_1\omega_2-\int_{\beta\alpha}\omega_1\omega_2= \begin{vmatrix} \int_\alpha\omega_1 & \int_\beta\omega_1\\ \int_\alpha\omega_2 & \int_\beta\omega_2 \end{vmatrix},$$ which is often nonzero. Therefore, iterated integrals are sensitive to the order, and they must capture some non-abelian information. But what kind of non-abelian information?
Differential equations and nilpotence
We can reformulate the definition of iterated integral as the element $y_r$ in the solution of a system of differential equations: \begin{align*} dy_0/dt &=0\\ dy_1/dt &=f_1\cdot y_0\\ dy_2/dt &=f_2\cdot y_1\\ \cdots & \\ dy_r/dt &=f_r\cdot y_{r-1} \end{align*} where we insist $y_0(t)\equiv 1$ so that $y_r$ agrees with our previous definition. The auxiliary functions $\{y_0,y_1,\cdots,y_{r-1}\}$ allow us to rewrite the system in the following way: $$ \frac{d}{dt}(y_0,y_1,\cdots,y_r)=(y_0,y_1,\cdots,y_r) \begin{pmatrix} 0 & f_1 & 0 & \cdots & 0 \\ 0 & 0 & f_2 & \ddots & \vdots \\ \vdots & \vdots & 0 & \ddots & 0 \\ \vdots & \vdots & \vdots & \ddots & f_r \\ 0 & 0 & 0 & \cdots & 0 \end{pmatrix} $$ where the matrix on the right is nilpotent (powers to 0). In general, the solutions to a system exist on a small scale for a short time locally. As the time progresses, the local information is being transferred globally. The global behaviour of the solutions is dictated by the system. In our case, iterated integrals are limited by the nilpotence property. Perhaps surprisingly, even with this limited non-abelian information, one finds they have interesting applications to number theory, most notably in Minyhong Kim's work, which uses $p$-adic iterated integrals (local) to help find rational points on curves (global).
Algebraic iterated integrals and beyond nilpotence
Elliptic curves and modular curves both feature prominently in the proof of Fermat's Last Theorem by Andrew Wiles and are extensively studied objects in number theory. My recent work (PhD thesis) constructs algebraic iterated integrals on elliptic curves and the modular curve (of level one). The construction proceeds in a similar fashion as iteratively solving the system of differential equations above. In the case of elliptic curves, my work is based on previous work of Levin--Racinet. The algebraic iterated integrals on elliptic curves lead naturally to elliptic polylogarithms, which generalizes classical polylogarithms \begin{align*} \mathrm{Li}_k(x):&=\sum_{n=1}^\infty\frac{x^n}{n^k},\qquad k\ge 1 \\ &=\int_0^x \frac{dz}{1-z}\underbrace{\frac{dz}{z}\cdots\frac{dz}{z}}_{(k-1)\text{ times}} \end{align*}
In the case of the modular curve, one needs to go beyond nilpotence, by adding some prescribed reductive (more complicated non-abelian) data, thereby constructing iterated integrals with coefficients. Specifically, algebraic iterated integrals of modular forms are constructed. They provide multiple modular values, which belong to a special class of numbers called periods. These periods appear not only in number theory, but also in quantum field theory, and in the study of motives. Francis Brown has proposed a framework where Galois theory of periods can be studied. Just as symmetries of algebraic numbers can be deduced from their defining equations, many relations between these periods result from structural properties of their defining iterated integrals. Our goal is to understand these structures and then connect them back to relations between periods.