Consider a function $f: X \rightarrow X$, an initial value $a_0 \in X$, and an iterative sequence $(a_n)$ given by
What can we say about the properties of $(a_n)$? For general $f$ and $X$ this is a relatively vague question, but constructions like this appear in a surprising variety of mathematical fields:
In Chaos Theory, the logistic map $f:[0,1] \rightarrow [0,1]$, $f(x)= rx(1-x)$ for some parameter $r \in [0,4]$, together with its iterative sequences $(*)$, gives a well-known example of a simple system displaying a large variety of dynamical behaviours and which is highly sensitive to initial values. Depending on the parameter $r$, we come across stable points and orbits and, eventually, chaotic behaviour. Nowadays, we also know many other maps from $[0,1]$ to itself which display deterministic chaos. Relatedly, iterative sequences also play a role in the construction of certain well-known fractals, such as the Cantor set.
In Number Theory, iterative sequences with $X=\mathbb{Z}$ and $f \in \mathbb{Z}[x]$ are of interest: Choose $f(x)=x^2-2x+2$ and $a_0 =3$, then $a_n=2^{2^n}+1$. Thus we obtain the sequence of Fermat numbers. Probabilistic arguments suggest that only finitely many of these numbers are primes, and that the same is true for any other iterative sequence generated from non-linear polynomials, provided the sequence is not eventually periodic. However, the resolution of this conjecture appears to be far out of the reach of current mathematics.
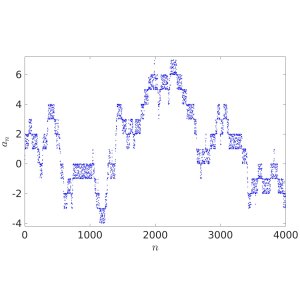
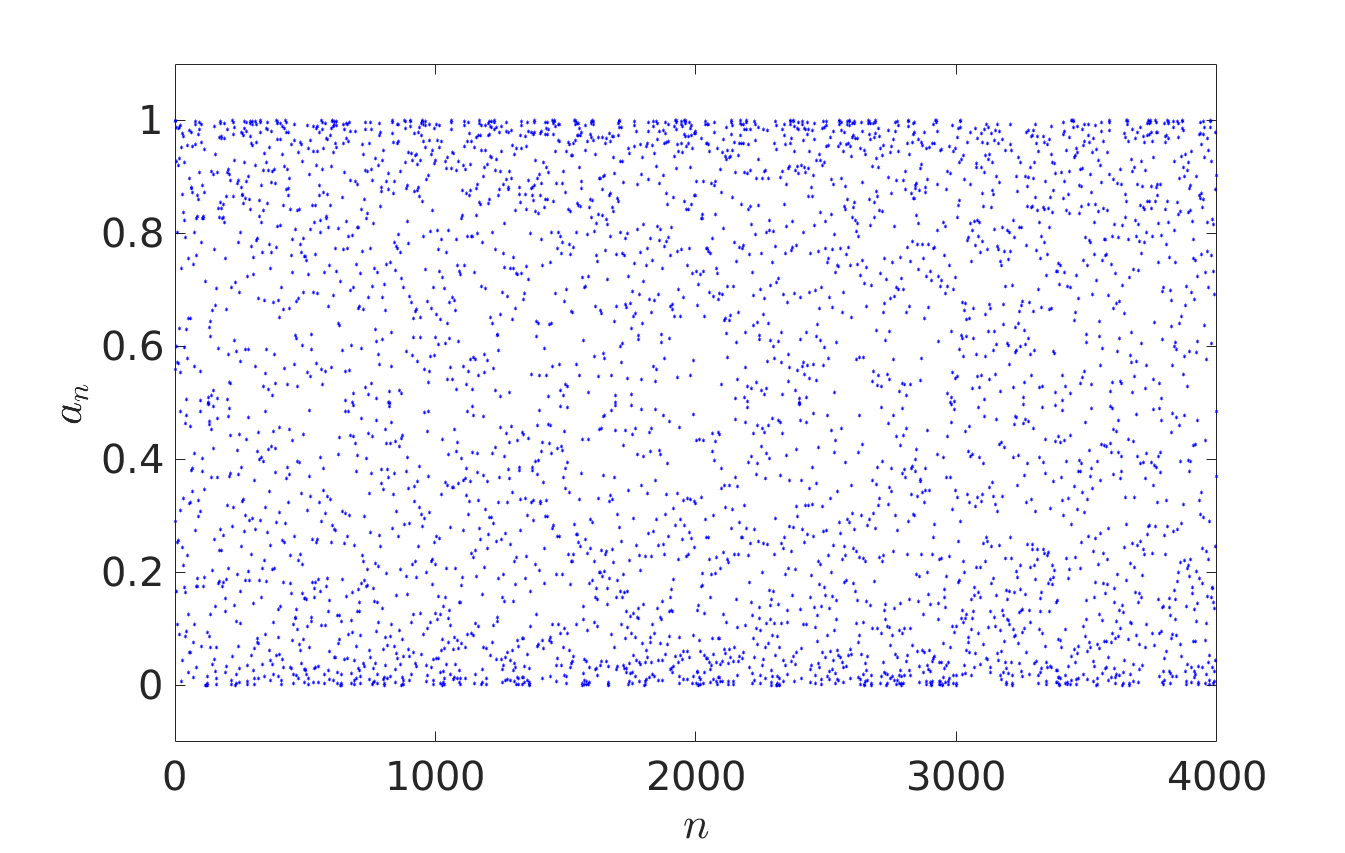
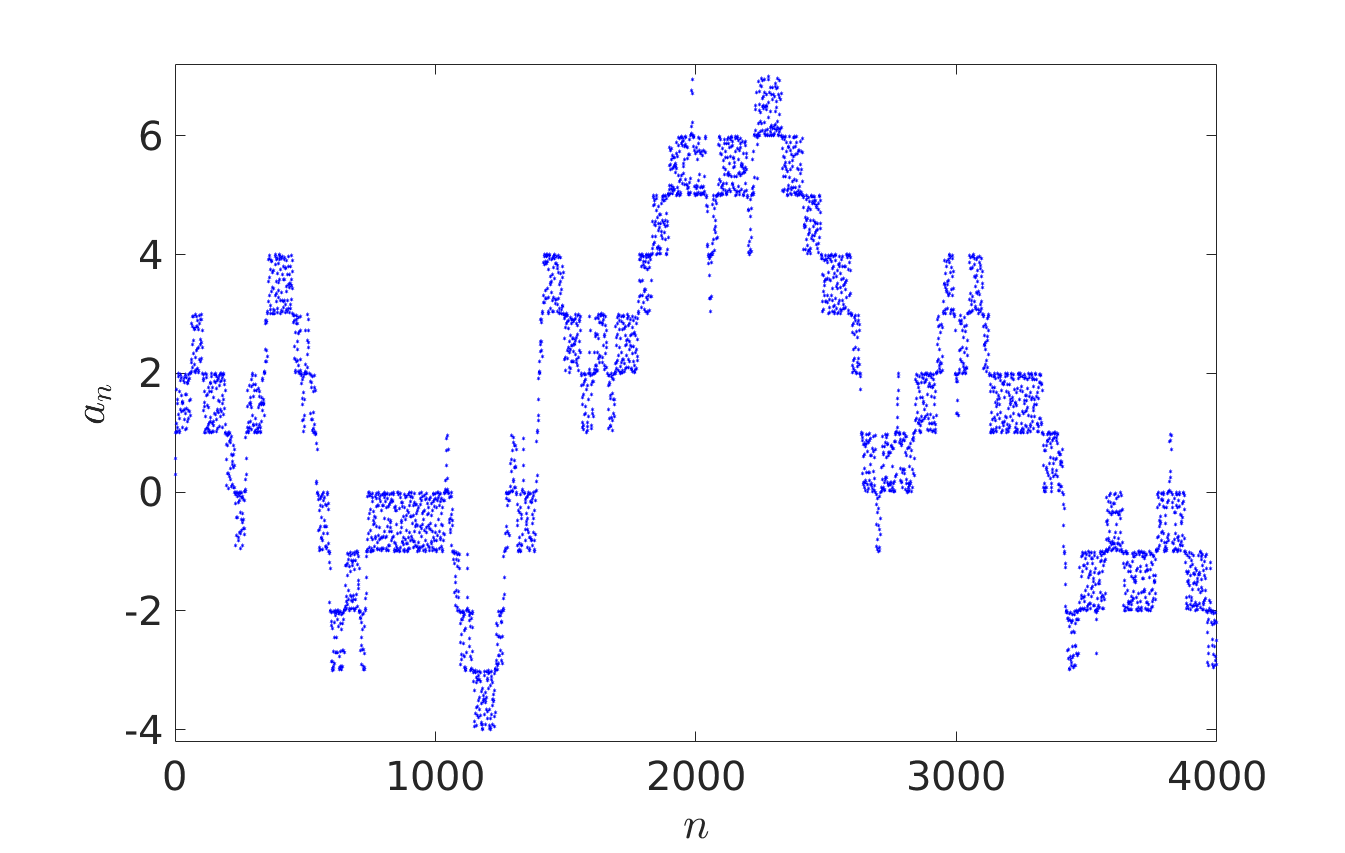
In Probability Theory, iterative sequence can give pseudorandom number generators or provide models for certain stochastic processes. In their recent paper [1], Oxford Mathematicians Julia Stadlmann and Radek Erban investigate limiting stochastic processes of iterative sequences $(*)$, where $X = \mathbb{R}$ and function $f: \mathbb{R} \rightarrow \mathbb{R}$ satisfies the shift-periodic property $f(x+1) = f(x)+1$. An example of such a function is given by $f(x) = x + c \sin (2 \pi x)$, where $c$ is an arbitrary constant. Considering $a_0 \in {\mathbb R}$, the first four thousand terms of iterative sequences $a_{n+1} = f(a_n)$ are plotted below. The right panel corresponds to a larger value of $c$ than the left one, allowing escape outside $[0,1]$.
We observe that the behaviour of iterates $a_{n+1} = f(a_n)$ looks random in the left panel and fills interval $[0,1]$ according to some non-uniform distribution law. In the right panel, the fractional parts $\{a_n\}$ of the iterative sequence appear to be distributed in $[0,1]$ according to the same law, but the behaviour of integer parts $\lfloor a_n \rfloor$ resembles more that of a random walk on $\mathbb{Z}$.
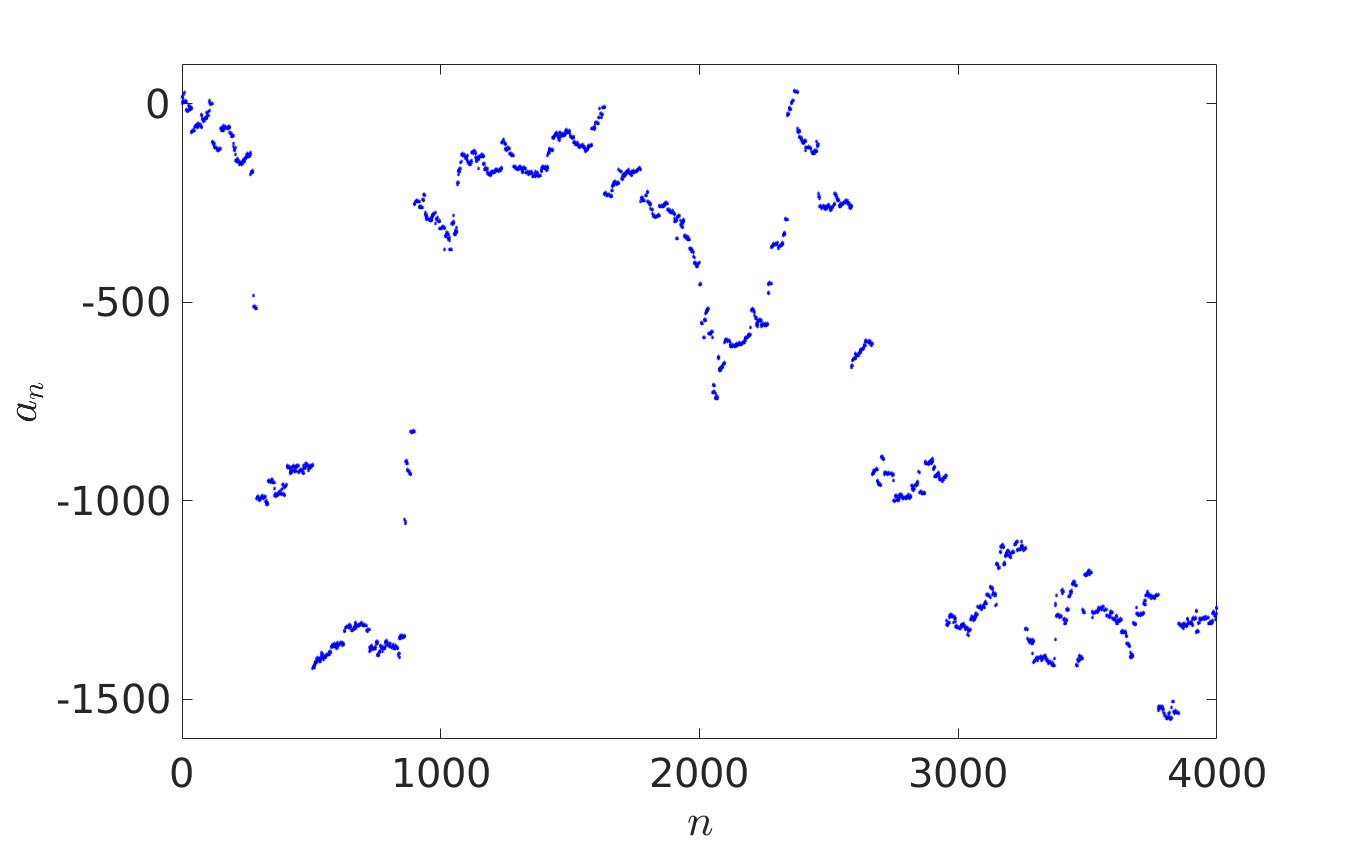
In [1], it is shown that general iterative sequences with the shift-periodic property display rich dynamical behaviour. They converge in certain limits to both discrete and continuous stochastic processes, including Brownian motion, more general Lévy processes and various types of random walks, depending on the properties of the generating shift-periodic map $f$, which we allow to have singularities. A natural example of such a shift-periodic map with singularities is given by $f(x) = x + \tan (2 \pi x)$ and in the panel on the right we plot one of its associated iterative sequences. The plot illustrates how for maps $f$ with singularities, we may observe a limiting stochastic process which is not Brownian motion (as is commonly the case for continuous $f$), but a more general Lévy process, including occasional large random jumps.
Understanding limiting stochastic properties of iterative sequences is of interest not only from a pure mathematical point of view, but it is also very useful in applications. For example, modern numerical algorithms for simulations of behaviour of biomolecules iteratively calculate their positions and velocities at the next time step from their positions and velocities in the previous time step. This process can be described by an iterative sequence $(*)$, where we identify $n$ with the time variable and take $a_n$ to be a large-dimensional vector of positions and velocities of all atoms in the system. Such molecular dynamics (MD) simulations can be used to study interactions between biomolecules in health and disease. Since MD simulations often include millions of atoms, they can result in very computationally intensive models. However, a lot of the simulated atomic coordinates describe water molecules. They provide a natural environment for biomolecules, but detailed trajectories of water molecules are of no special interest. If we look at the behaviour of a biomolecule itself, we observe that it follows a stochastic process. The biomolecule as a whole, and also its parts, appear to undertake random walks, appear to be subject to probabilistic description. What type of stochastic processes do MD simulations converge to? How can we describe them in simple terms? Researchers in the Mathematical Institute study such questions and use their answers to design efficient methodologies for simulating biomolecules and living systems, see, for example, reference [2] for a recent work on stochastic coarse-grained models derived from MD simulations.
References:
[1] J. Stadlmann and R. Erban, "Limiting stochastic processes of shift-periodic dynamical systems," Royal Society Open Science (2019)
[2] R. Erban, "Coarse-graining molecular dynamics: stochastic models with non-Gaussian force distributions," Journal of Mathematical Biology (2019)