Networks provide powerful tools and methods to understand inter-connected systems. What is the most central element in a system? How does its structure affect a linear or non-linear dynamical system, for instance synchronisation? Is it possible to find groups of elements that play the same role or are densely connected with each other? These are the types of questions that can be answered within the realm of network science. For standard algorithms to be used, however, it is usually expected that the underlying network structure is known. Yet, there are many situations where the connections between the nodes are completely hidden, and where only certain signals on the nodes can be observed. This is for instance the case in network neuroscience or financial networks, where time series are observed on nodes that are assumed to be connected by hidden functional relations.
Current methods for analysing such hidden networks involve a succession of steps whose outcome is highly sensitive to specific design decisions: choose a measure for the similarity between pairs of time series; convert the resulting similarity matrix into a graph, often by means of thresholding; finally apply a network algorithm. This approach is unsatisfying for many reasons. For instance, when the number N of time series is large, it implies calculating a prohibitive N^2 pairs of similarities, in contrast with the usual sparsity of the data or its low rank. Conceptually, each step of the three-stage process generally computes point estimates and discards any notion of uncertainty such that it is difficult to distinguish genuine structure from noise.
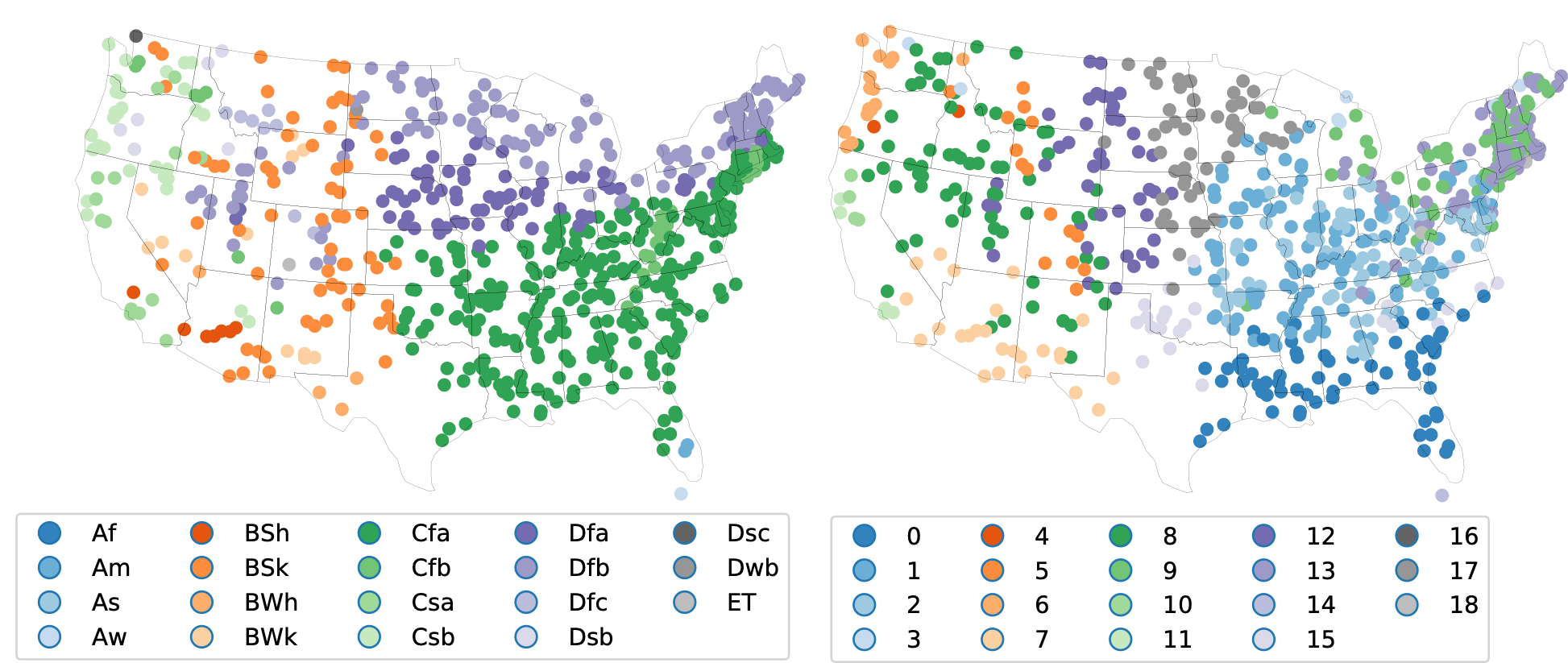
A recent publication by Oxford Mathematician Renaud Lambiotte in Science Advances, in collaboration with researchers from Imperial College, Spotify and Université catholique de Louvain, proposes a radically new way to consider the problem. Focusing on community detection, the problem of finding groups of densely connected nodes in networks, the authors propose a Bayesian hierarchical model for multivariate time series data that provides an end-to-end community detection algorithm and propagates uncertainties directly from the raw data to the community labels. This shortcut is more than a computational trick, as it naturally allows for the extraction of communities even in the case of short observation time windows. The method is validated on synthetic data, and on financial and climate time series. As an illustration, the following figure shows the clustering of climate zones in the US based, on the left, on the classical Koppen-Geiger climate classification system and, on the right,using the new method, on the monthly average high and low temperatures and precipitation amounts.