Oxford Mathematician Weijun Xu talks about his exploration of the universal behaviour of large random systems:
"Nature comes with a separation of scales. Systems that have apparently different individual interactions often behave very similarly when looked at from far away. This phenomenon is particularly attractive when randomness is involved.
A well-known example is the classical central limit theorem, which states that a sequence of independent, identically distributed random variables sum up and rescale to Gaussian distribution, regardless of their individual distributions.
A dynamic version of this is Donsker's invariance principle, which states that random walks with independent steps rescale to Brownian motion, regardless of the distribution of individual steps. In these two cases, Gaussian distributions and Brownian motion are universal laws that describe large scale behaviour of a large class of microscopic models with independent components.
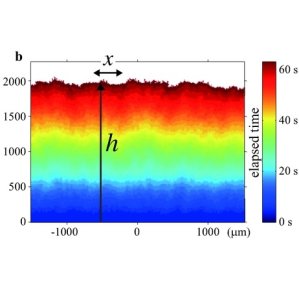
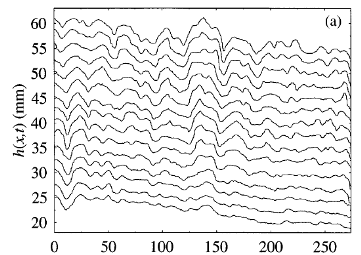
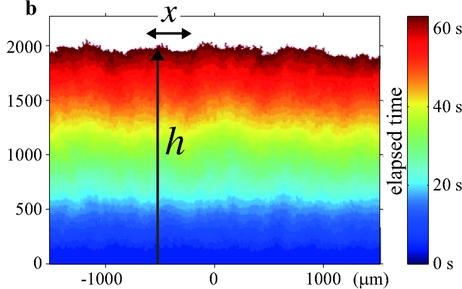
Universal phenomena also appear in many other situations. For example, the following images show the large scale behaviour of three very different interface growth models.
The left most one comes from the interface in burning a paper, the middle one describes the boundary between two turbulent states in a liquid crystal, while the right one is the height of a tetris game. Yet these three interfaces look essentially the same when zoomed out from far away!
Image 1: Maunuksela et al. Image 2: Takeuchi et al. Image 3: Hairer
Mathematically, such microscopic interface growth/fluctuation could be modelled by the stochastic partial differential equation of the form \begin{equation*} \partial_t h = \partial_x^2 h + \sqrt{\varepsilon} F(\partial_x h) + \eta\;, \end{equation*} where $\partial_x^2$ is a smoothing mechanism in microscopic scale, the nonlinearity $F$ describes the growth mechanism, and $\eta$ is a space-time random process that influences the evolution. In this equation, different interface growth mechanisms are modelled by different nonlinear symmetric function $F$. In a joint work with Hairer, which is based on this previous work, we showed that for rather arbitrary functions $F$, the large scale version of $h$ defined by \begin{equation*} h_{\varepsilon}(t,x) := \sqrt{\varepsilon} h(t/\varepsilon^2, x/\varepsilon) - C_\varepsilon t \end{equation*} converges to the KPZ equation, formally given by \begin{equation*} \partial_t H = \partial_x^2 H + \lambda (\partial_x H)^{2} + \xi - \infty\;, \end{equation*} where the coefficient $\lambda$ depends on $F$ in a nontrivial way. In other words, the large scale behaviour of $h$ is universal - the nonlinear mechanism is always square of the derivative whatever the microscopic mechanism $F$ is!
Universalities of this type also arise in many other situations. They still remain largely mysterious and their mystery is an active challenge in mathematics and physics."