Oxford Mathematician Francis Bischoff talks about his recent work on generalized Kähler geometry and the problem of describing its underlying degrees of freedom.
"Kähler manifolds are important geometric structures which play a central role in supersymmetric quantum field theories and mirror symmetry. These areas of research are at the forefront of modern geometry. A Kähler structure is a manifold equipped with a Riemannian metric $g$, and a compatible complex structure $I$. You can think of a metric as a structure on a manifold which allows you to measure lengths and angles, while a complex structure lets you define complex-valued coordinate functions on the manifold in a consistent way.
A striking feature of a Kähler metric is that it involves drastically less information than an ordinary Riemannian metric. To see this, let's describe a general Riemannian metric in a small region surrounding a point on an $n$-dimensional manifold. We can do this by representing the metric as a symmetric $n \times n$ matrix of functions, in the following way: \[ g = \begin{pmatrix} g_{11} & g_{12} & \ldots & g_{1n} \\ g_{21} & g_{22} & \dots & g_{2n} \\ \vdots & \vdots & \ddots& \vdots \\ g_{n1} & g_{n2} & \ldots & g_{nn}\end{pmatrix}, \qquad g_{ij} = g_{ji}. \] If we now count up the independent component functions $g_{ij}$, remembering that $g_{ij} = g_{ji}$, then we see that there are $\frac{1}{2}n(n + 1)$ of them. This number grows quickly with the dimension. For example, on a $4$-dimensional manifold, the metric already involves $10$ independent components.
On the other hand, a Kähler metric can be reduced to a single function $K$. To do this, we start by choosing complex coordinate functions $z_{i}$ using the complex structure $I$. Then, we calculate the components of the metric by taking derivatives of the function, as follows: \[ g_{i \bar\jmath} = \frac{\partial^2 K}{\partial z_{i} \partial \bar{z}_{j} }. \] This function is called the Kähler potential, and it represents a major simplification in our understanding of the geometry, with important practical consequences. For example, the Kähler potential is used in an essential way in the search for metrics with special curvature properties, since it allows these problems to be reduced to differential equations involving a single function.
In 1984, physicists discovered a more general class of geometric structures, now known as generalized Kähler (GK) geometry. These are expected to play a role in quantum field theories which are similar to those which make Kähler geometry so exciting. A GK structure is a Riemannian manifold equipped with 2 distinct complex structures $I_{+}$ and $I_{-}$, which satisfy a modified compatibility condition. A natural question which has existed since their discovery asks whether GK metrics can also be reduced to a single function, or generalized Kähler potential. In fact, this is predicted on physical grounds, and there have been constructions of special examples of GK potentials in the physics literature.
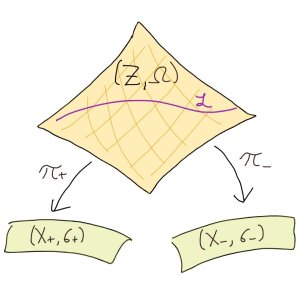
It turns out that a general solution to this problem lies in a reformulation of Kähler geometry put forward by S. Donaldson. In his approach, a Kähler structure is represented by a submanifold $\cal{L}$ inside a larger space $Z$, which is equipped with a holomorphic symplectic structure $\Omega$. The metric $g$ itself corresponds to the submanifold $\cal{L}$, which has the special property of being Lagrangian for the imaginary part of $\Omega$. This is in line with the famous dictum of A. Weinstein that 'everything is a Lagrangian submanifold'. And since Lagrangians are known to be reducible to a single function, this explains the origin of the Kähler potential.
In recent work together with M. Gualtieri and M. Zabzine, we show that Donaldson's approach extends to the setting of generalized Kähler geometry. Namely, a GK structure (of symplectic type) may also be represented by a submanifold $\cal{L}$ inside a holomorphic symplectic manifold $(Z, \Omega)$, with the property that $\cal{L}$ is Lagrangian with respect to the imaginary part of $\Omega$. The spaces $(Z, \Omega)$ that show up in our description are more general than in the Kähler case. They are known as Morita equivalences and we need to rely on the theory of Poisson geometry to construct them. An upshot of this reformulation is that a GK metric corresponds to a Lagrangian submanifold, and therefore, it can be reduced to a single function. In this way, we solve the long standing problem of describing a GK metric in terms of a generalized Kähler potential."