Oxford Mathematician Anna Seigal talks about her work on connecting invariant theory with maximum likelihood estimation.
"A widespread problem in statistics is to fit a model to data. Given a model, which is believed to describe some data, the point in the model that best fits the data is sought. This point is called the maximum likelihood estimate (or MLE) given the data. For example, the probability of surviving a disease can be estimated from a sample of people who have had the disease: the MLE is obtained by dividing the number of people who survived by the total number of people in the sample. Another example of an MLE is to find a line of best fit that relates two variables, assuming one variable depends linearly on the other.
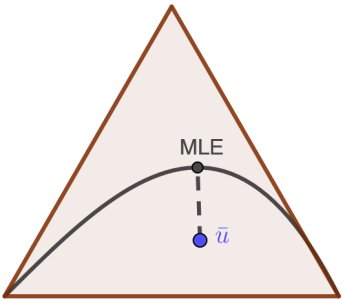
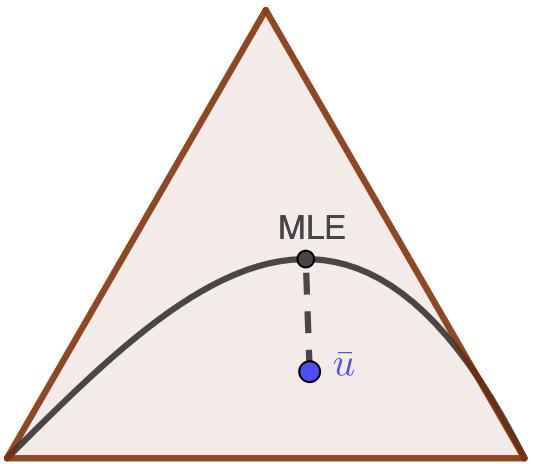
Often statistical models are more complicated structures than straight lines, as in the following picture. A statistical model, represented by the black curve, lies in a space, represented by the red triangle. The observed data gives the blue point $\bar{u}$ in the space. The MLE is a point in the model that is closest to the data, in the sense that it was most likely to give rise to the observed data.
Many different approaches can be used to search over a model to find a good fit to data. There is growing interest in understanding the mathematical structure that underpins maximum likelihood estimation. This structure allows us to obtain theoretical guarantees, and to answer questions such as: how can we test that we have reached an optimal point in the model? How many optimal points do we expect to find? How much data is required before the MLE can even exist?
In a recent preprint we apply algebraic methods from invariant theory to the problem of maximum likelihood estimation in various statistical models: log-linear models in the discrete setting and multivariate Gaussian models in the continuous setting. We describe algebraic approaches to finding the MLE, and we characterise when the MLE exists, in terms of orbits of points under group actions.
Classically, invariant theory studies orbits under group actions, orbit closures, and the equations that vanish on them. The orbit of a point under a group is the set of points that can be obtained from it by acting by a group element. We can summarise information about an orbit using notions of stability. For example, a point that can be scaled arbitrarily close to zero under a group action is called unstable. These invariant theory structures were studied classically by mathematicians including David Hilbert and Emmy Noether. More recently, numerical and algorithmic approaches to study the stability of points under group actions have become possible.
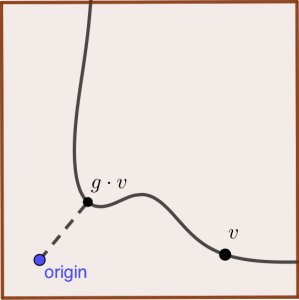
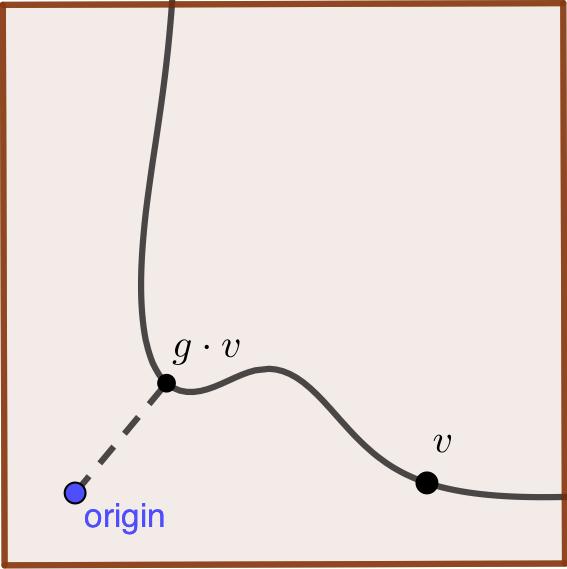
This picture describes our invariant theory set-up. We have an orbit of a point under the action of a group, represented by the black curve in the picture. The orbit lies inside a space, represented by the red square. For each point in the orbit, we can compute its distance to the origin. We seek the point in the orbit that is closest to the origin. Another way to say that a point is unstable is that this distance to the origin gets arbitrarily small, i.e. the orbit contains the origin in its closure.
In our preprint, we build a dictionary that translates between these two pictures: between properties of the MLE (such as existence and uniqueness) and stability of a corresponding orbit under a group action. This connection enables us to find new conditions for MLE existence, as well as suggesting a more general class of statistical models, which we call Gaussian group models.
This research is joint work with Carlos Améndola at TU Munich, Kathlén Kohn at KTH Stockholm, and Philipp Reichenbach at TU Berlin. Although we most enjoyed working on the project together in person, we were still able to have a good time when finishing our preprint under strict social distancing (with a closest pairwise distance of more than 300 miles)."