Oxford Mathematician Katherine Staden talks about the mathematics of seating plans.
The Oberwolfach Institute is a famous venue for mathematical conferences and events. Its dining hall contains some circular tables of various sizes; I don't know how big they are but I know they seat $n$ people in total. I'm inviting $n$ people to a conference, and to foster good communication, I want to write some seating plans so that each pair of people sit next to each other exactly once during dinner. Is this possible?
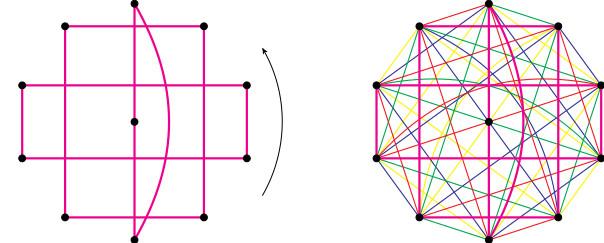
This question was posed by Ringel in 1967 and despite attracting a lot of attention among mathematicians, was unsolved until recently. It has an equivalent formulation in terms of a mathematical object called a graph, or network, which is a collection of points, some of which are joined by lines (edges). Form a complete graph $K_n$ by letting each person be a point and join every pair by an edge (to represent every possible pair of people). Now give each day of the conference, i.e. each required seating plan, a colour $c_1,...,c_\ell$. Since each person needs to sit next to $n-1$ other people, and she sits next to $2$ of them at each meal, we need $\ell=\frac{n-1}{2}$ colours, and $n$ needs to be odd. So we want to colour the edges of $K_n$ with $\frac{n-1}{2}$ colours so that the edges in each colour look like the layout of the tables (see figure). This is called a graph decomposition problem.
Figure: tables of sizes $3,4,4$ and a corresponding colouring of $K_{11}$.
If $n$ is very small, a simple brute-force algorithm can solve the problem on a computer. If there is a single table it was already solved by Walecki in 1892, predating the conjecture, but it was not until 2013 that Traetta solved the two-table problem. In these cases and in much of the work on the problem, researchers were able to explicitly describe the seating plans, by finding one special seating plan and 'rotating' it to find the others. It turned out to be hard to apply this constructive approach to the general problem where the collection of tables is arbitrary. Eventually in 2018 Glock, Joos, Kim, Kühn and Osthus were able to solve the problem for large $n$ using a non-constructive method that uses random choices to find the seating plans. My recent work with fellow Oxford Mathematician Peter Keevash solved the 'generalised Oberwolfach problem', where every day the collection of tables is allowed to change (as long as they still seat $n$). Both are examples of mathematical results which show that a solution exists without actually exhibiting it. Unfortunately neither of these two solutions would be any use for a real-life seating plan problem as the number $n$ of people is far larger than any conference will ever be!
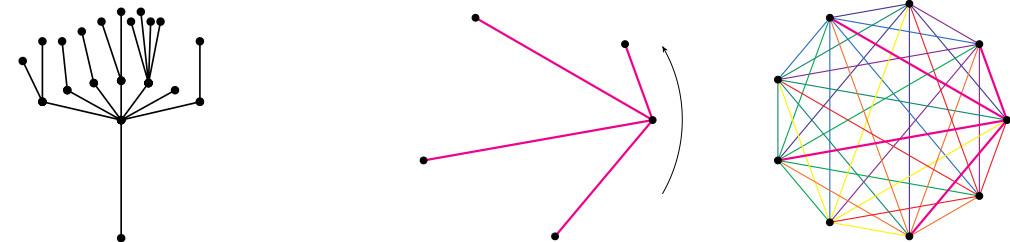
The Oberwolfach problem is actually one of many graph decomposition problems, which, while typically without practical application, are interesting in their own right, and which allow the tools developed to solve the Oberwolfach problem be tested further. One of these problems was also posed by Ringel, in 1963, who conjectured that there should exist a colouring of the edges of $K_n$ where now the edges in each colour should look like any given tree $T$ on $\frac{n+1}{2}$ points, where here $n$ is odd. A tree is any graph in which it is always possible to get between any two points by following edges, but you can only get back to where you started by backtracking (the figure should explain its name).
Figure: a tree, a star $T$ with $5$ points and corresponding colouring of $K_9$.
This time, it turns out we need $n$ colours. Again, if $T$ has a simple structure, or if $n$ is small, the problem can be easy. The picture shows how to find a colouring when $T$ has one point in every edge (a star). But the structure of $T$ could be very complicated; the challenge in solving Ringel's conjecture is to find a proof that works for every $T$.
My recent work with Peter Keevash proves the conjecture, which has also been proved in independent work of Montgomery, Pokrovskiy and Sudakov. As well as tools from graph theory, we use ideas from probability - for example we will often choose an edge at random from among a set of choices and colour it - and design theory.
There is still much more to understand regarding graph decompositions and there are a great many tantalising open problems. Perhaps the next step is the following conjecture of Gyárfás from 1976: given trees $T_1,\ldots, T_{n}$ where $T_i$ contains $i$ points, can you colour the edges of $K_{n}$ with $n$ colours so that the edges in colour $i$ look like $T_i$?"