For thirty years Oxford Mathematician Roger Penrose has challenged one of the key planks of Cosmology, namely the concept of Inflation, now over 40 years old, according to which our universe expanded at an enormous rate immediately after the Big Bang. Instead, fifteen years ago, Penrose proposed a counter-concept of Conformal Cyclic Cosmology by which Inflation is moved to before the Big Bang and which introduces the idea of preceding aeons. The concept has been disputed by most physicists, but Roger and colleagues believe that new evidence has come to light which requires closer inspection and argument - the research is published today in the Monthly Notices of the Royal Astronomical Society (MNRAS).
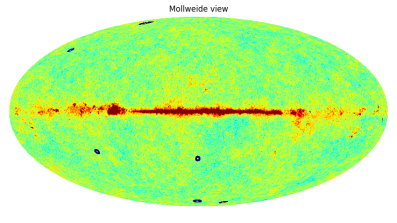
Recent analysis of the Cosmic Microwave Background (CMB) by Roger, Daniel An, Krzysztof Meissner and Pawel Nurowski has revealed, both in the Planck and WMAP satellite data (at 99.98% confidence), a powerful signal that had never been noticed previously, namely numerous circular spots $\sim 8$ times the diameter of the full moon. The brightest six (Figure 1) are $\sim 30$ times the average CMB temperature variations seen at precisely the same locations in the Planck and WMAP data. These spots were overlooked previously owing to a belief that the very early exponentially expanding inflationary phase of standard cosmology should have obliterated any such features.
(Figure 1: CMB sky, marking 6 most prominent raised-temperature circular spots, found both in Planck and WMAP data; argued to be results of Hawking radiation from supermassive black holes in a previous aeon)
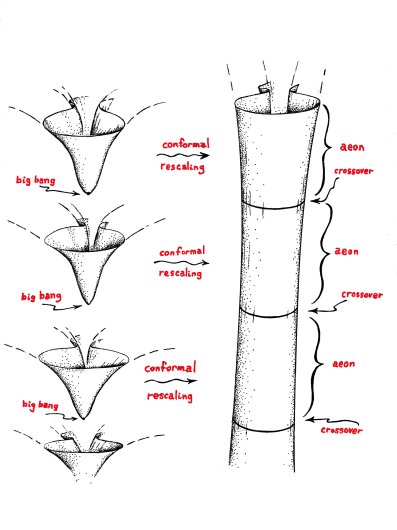
There are alternative universe models without inflation, but most encounter fundamental difficulties in not accounting for CMB features normally explained by inflation. However, Conformal Cyclic Cosmology (CCC) does so, by displacing 'inflation' to before the Big Bang - as the exponentially expanding remote future of an earlier cosmic aeon. This 'aeon' is a universe epoch, resembling what we currently perceive to be the entire history (without inflation) of our Universe. In CCC, there is an infinite succession of such aeons, each having a big-bang origin which is the conformal continuation or the exponentially expanding remote future of the preceding aeon (Figure 2). Conformal geometry allows for stretching or squashing of the metric structure, and is the geometry respected by a physics without mass (such as Maxwell's electromagnetism). This applies both to the remote future and big bang of each aeon, so the matching of aeon to aeon makes geometrical sense - and also physical sense because the conformal squashing of the cold low-density remote future matches the conformal stretching of the hot dense big bang of the subsequent aeon.
(Figure 2: Cartoon of conformal cyclic cosmology: each aeon's big bang arises from the conformally compressed remote future of its preceding aeon)
The exceptions to this smooth conformal matching are the supermassive black holes in an aeon's remote future, which would each have almost completely swallowed its surrounding galactic cluster, before eventually evaporating away entirely into Hawking radiation (after perhaps $10^{106}$ years). However, by conformal squashing, all this radiated energy comes through into the succeeding aeon at a single 'Hawking point.' The emerging photons then scatter within an expanding region, but do not become free until $\sim 380000$ years later, when finally appearing in the CMB of that subsequent aeon. This spread-out region would look to us like a disc ∼ 4° across, i.e. $\sim 8$ times the diameter of our full moon, an effect that we appear to be actually seeing in our own CMB sky.
Roger talks about his work in this November 2018 Oxford Mathematics Public Lecture.