A set of integers greater than 1 is primitive if no number in the set divides another. Erdős proved in 1935 that the series of $1/(n \log n)$ for $n$ running over a primitive set A is universally bounded over all choices of A. In 1988 he conjectured that the universal bound is attained for the set of prime numbers. In this research case study, Oxford's Jared Duker Lichtman describes recent progress towards this problem:
"On a basic level, number theory is the study of whole numbers, i.e., the integers $\mathbb{Z}$. Maturing over the years, the field has expanded beyond individual numbers to study sets of integers, viewed as unified objects with special properties.
A set of integers $A\subset \mathbb{Z}_{>1}$ is primitive if no number in $A$ divides another. For example, the integers in a dyadic interval $(x,2x]$ form a primitive set. Similarly the set of primes is primitive, along with the set $\mathbb{N}_k$ of numbers with exactly $k$ prime factors (with multiplicity), for each $k\ge1$. Another example is the set of perfect numbers $\{6,28,496,..\}$ (i.e. those equal to the sum of their proper divisors), which has fascinated mathematicians since antiquity.
After Euler's famous proof of the infinitude of primes, we know $\sum_p 1/p$ diverges, albeit "just barely" with \begin{align*} \sum_{p\le x}\frac{1}{p} \sim \log\log x. \end{align*} On the other hand, we know $\sum_p 1/p\log p$ converges (again "just barely"). Using the notation \begin{align*} f(A) := \sum_{n\in A}\frac{1}{n\log n}, \end{align*} we have $f(\mathbb{N}_1)<\infty$. In 1935 Erdős generalized this result considerably, proving $f(A) <\infty$ uniformly for all primitive sets $A$. In 1988 he further conjectured the maximum is attained by the primes $\mathbb N_1$:
Conjecture 1. $f(A) \leq f (\mathbb{N}_1)$ for any primitive $A$.
Note we may compute $f(\mathbb N_1) = \sum_p 1/p\log p \approx 1.6366$.
Since 1993 the best bound has been $f(A) < 1.84$, due to Erdős and Zhang. Recently, Carl Pomerance and I improved the bound to the following:
Theorem 1. $f (A) < e^\gamma \approx 1.78$ for any primitive A, where $\gamma$ is the Euler-Mascheroni constant.
Further $f(A) < f(\mathbb{N}_1)+0.000003$ if 2 lies in $A$.
One fruitful approach towards the Erdős conjecture is to split up $A$ according to the smallest prime factor, i.e., for each prime $q$ we define $$A_q = \{ n \text{ in } A : n \text{ has smallest prime factor } q\}.$$
We say $q$ is Erdős strong if $f(A_q)\le f(q)$ for all primitive $A$. Conjecture 1 would follow if every prime is Erdős strong, since then $f(A) = \sum_q f(A_q) \le f(\mathbb{N}_1)$.
Unfortunately, we don't know whether $q=2$ is Erdős strong, but we showed that the first hundred million odd primes are all Erdős strong. And remarkably, assuming the Riemann hypothesis, over $99.999973\%$ of primes are Erdős strong.
Primitive from perfection
In modern notation, a number $n$ is perfect if $\sigma(n)=2n$ where $\sigma(n) = \sum_{d\mid n}d$ is the full sum-of-divisors function. Similarly $n$ is called deficient if $\sigma(n)/n<2$ (abundant if $>2$).
Since $\sigma(n)/n$ is multiplicative and $>1$, we see that perfect numbers form a primitive set, along with the subset of non-deficient numbers $n$ whose divisors $d\mid n$ are all deficient.
It is a classical theorem that non-deficient numbers have a well-defined, positive asymptotic density. This was originally proven with heavy analytic machinery, but Erdős found an elementary proof by using primitive non-deficient numbers (this density is now known $\approx 24.76\%$). His proof led him to introduce the notion of primitive sets and study them for their own sake.
This typified Erdős' penchant for proving major theorems by elementary methods.
A related conjecture of Banks & Martin
Recall $\mathbb{N}_k$ denotes the set of numbers with $k$ prime factors. In 1993, Zhang proved $f (\mathbb{N}_k) < f (\mathbb{N}_{1})$, which inspired Banks and Martin to predict the following:
Conjecture 2. $f (\mathbb{N}_k) < f (\mathbb{N}_{k-1})$ for each $k > 1$.
They further predicted that, for a set of primes $\mathcal Q$, \begin{align*} f\big(\mathbb{N}_k(\mathcal Q)\big) < f\big(\mathbb{N}_{k-1}(\mathcal Q)\big)\qquad\textrm{for each } k>1 \end{align*} where $A(\mathcal Q)$ denotes the numbers in $A$ composed of primes in $\mathcal Q$. Banks and Martin managed to prove this conjecture in the special case of sufficiently "sparse'' subsets $\mathcal Q$ of primes.
This result, along with Conjectures 1 & 2, illustrates the general view that $f(A)$ reflects the prime factorizations of $n\in A$ in a quite rigid way.
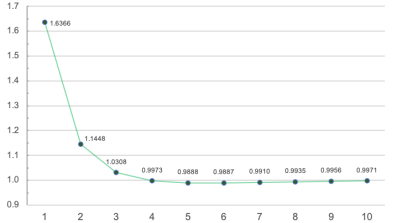
Beautiful though this vision of $f$ may be, it appears reality is more complicated. Recently I precisely computed the sums $f(\mathbb{N}_k)$ (see Figure 1 below) and obtained a surprising disproof of Conjecture 2!
Theorem 2. $ f( \mathbb{N}_k) > f(\mathbb{N}_6) $ for each $k\neq 6$.
Figure 1. Plot of $f(\mathbb{N}_k)$ for $k=1,2,..,10$.
I also proved $\lim_{k\to\infty} f(\mathbb{N}_k) = 1$, confirming a trend observed in the data. However, much about this data remains conjectural. For instance, the sequence $\{f(\mathbb{N}_k)\}_{k\ge6}$ appears to increase monotonically (to 1), and the rate of convergence appears to be exponential $O(2^{-k})$, while only $O(k^{\varepsilon-1/2})$ is known. Similar phenomena seem to occur when experimenting with subsets $A\subset \mathbb{N}_k$ of e.g. even, odd, and squarefree numbers.
I hope this note illustrates Erdős' conjecture spawning new lines of inquiry. For example, researchers are now studying variants of the problem in function fields $\mathbb{F}_q[x]$. Also, in forthcoming work with Chan and Pomerance, we manage to prove Conjecture 1 for 2-primitive sets $A$, i.e., no number in $A$ divides the product of 2 others.
The full Erdős conjecture has remained elusive, but working towards it has led to interesting developments. In the words of Piet Hein:
Problems worthy of attack prove their worth by fighting back.