Oxford Mathematician Vidit Nanda discusses his recent work with colleagues Bernadette Stolz, Jared Tanner and Heather Harrington on detecting singularities in data.
"Fitting geometric models to high-dimensional point clouds plays an essential role in all sorts of tools in contemporary data analysis, from linear regression to deep neural networks. By far the most common and well-studied geometric models are manifolds. For instance, the plane, sphere and torus illustrated below are all two-dimensional manifolds that can be embedded in three-dimensional Euclidean space.
There is a local test which characterizes d-dimensional manifolds: around each point, can you find a small region which resembles standard d-dimensional Euclidean space? If the answer is yes, then you have a d-manifold on your hands. Thus, if we were to zoom in with a very high-powered microscope at any point on the sphere or torus, we would approximately see a plane.
When confronting heterogeneous data which comes from several different sources or measurements, it may no longer be feasible to expect that a single underlying manifold will provide a good fit to all the data points. This is because the union of two d-dimensional manifolds (such as a sphere and a plane) along a shared sub-manifold (such as an equator) will not itself be a d-manifold. If you examine small neighbourhoods around points in the common sub-manifold, you can see that they will fail the local test for manifold-ness. For instance, if you zoom in on any point lying in the equator of the figure below, you will see two planes that intersect along a common line rather than a single plane.
Such non-manifold spaces which are built out of manifold pieces are called stratified spaces, and their non-manifold regions, such as the equator in the example above, are called singularities. The study of stratified spaces has been a long and fruitful enterprise across several disciplines in pure mathematics, including algebraic geometry, algebraic topology and representation theory.
We have recently developed a framework to automatically detect singularities directly from data points even when none of the data points lie exactly on the singular regions. One key advantage is that we are now able to partition a heterogeneous dataset into separate clusters based on their intrinsic dimensionality. Thus, a dataset living on the plane-plus-sphere described above would be decomposed into five clusters, one of which lives near the one-dimensional singular equator, while the other four lie on various parts of the sphere or the plane.
All five pieces are manifolds, so the standard manifold-fitting techniques which are pervasive in data science can be safely applied to them individually.
The key technique in this singularity-detection framework is persistent cohomology, which assigns a family of combinatorial invariants called barcodes, one for each dimension, to a collection of data points. If these points have been sampled densely from a d-dimensional sphere, then there is a prominent bar in the d-th persistent cohomology barcode and not much else. Given each point p in the dataset, one examines the set of all annular neighbours - this consists of all data points q satisfying α < dist(p,q) < β for some small positive distances α and β, where dist denotes Euclidean distance. By the local manifold property, the central point p lies on a d-dimensional manifold, then for suitably small α < β the set of all annular neighbours will live approximately on a (d-1)-dimensional sphere, which can be detected accurately by the presence of a single dominant bar in the (d-1)-st persistent cohomology barcode.
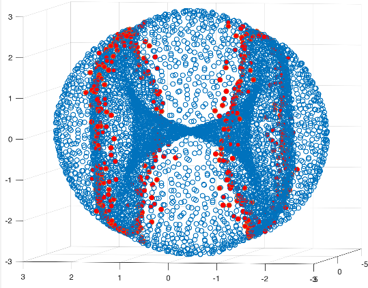
We tried this technique on a dataset whose points correspond to configurations of a molecule called cyclo-octane. The data consists of 5000 points in 24-dimensional space, and the points live on the intersection of two embedded surfaces along two circles. As expected, points lying near the two singular circles are easily identified by their local persistent cohomology barcodes. These special points are coloured red in the 2-dimensional projection of the data below."