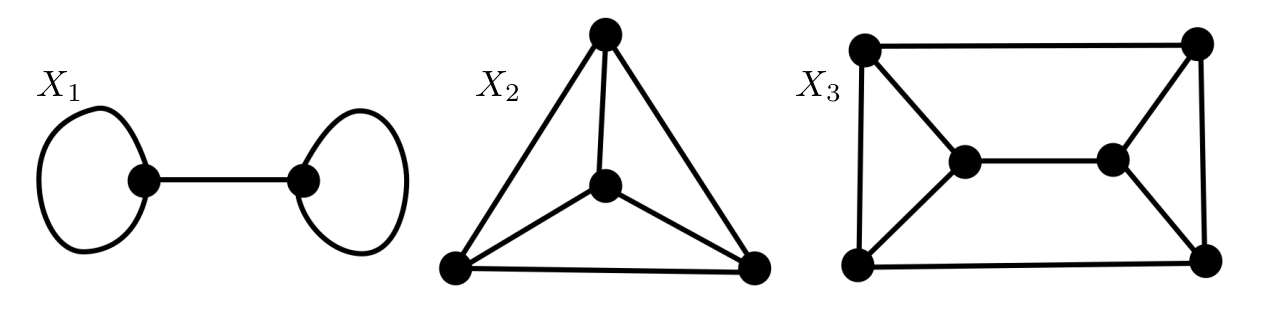Oxford Mathematician Daniel Woodhouse talks about the theorem that motivates much of his research.
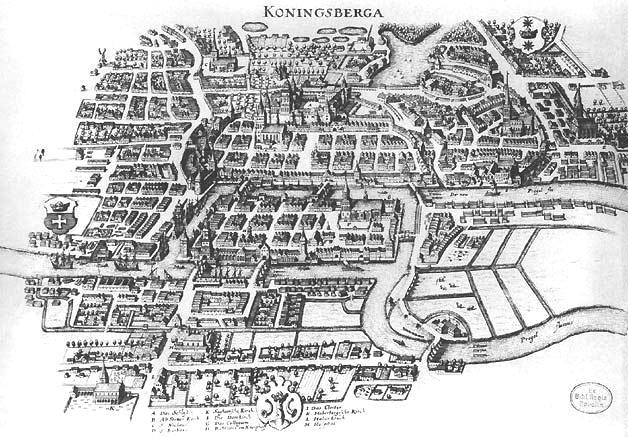
"According to lore, denizens of the Prussian city of Königsberg would spend their Sunday afternoons wandering the streets. From this pastime came a puzzle - could a wanderer cross each of the city's seven bridges without crossing the same bridge twice? The path of the River Pregel divides the city into four distinct regions, including a central isolated island, so the question was more complicated than a matter of crossing back and forth from one side of a river to the other.
If a positive solution existed, then someone would surely have found it, so it could be guessed that the answer was negative. In principle, you could write down an exhaustive list of all possible sequences of bridge crossings, but this would be a very crude kind of proof. The problem eventually came to the attention of Leonhard Euler, who set about finding an explanation that offered more insight into the nature of the problem. In 1736 Euler wrote up his solution, providing arguments that not only applied to the bridges of Königsberg, but to any arrangement of rivers and bridges. Initially, it seems from his correspondence that Euler was inclined to dismiss the intellectual merits of the problem, not regarding it as mathematical at all. But in the introduction of his paper he declares it to belong to a kind of mathematics only previously speculated: the geometry of position ("Geometriam situs''). Today this kind of mathematics is better known as topology.
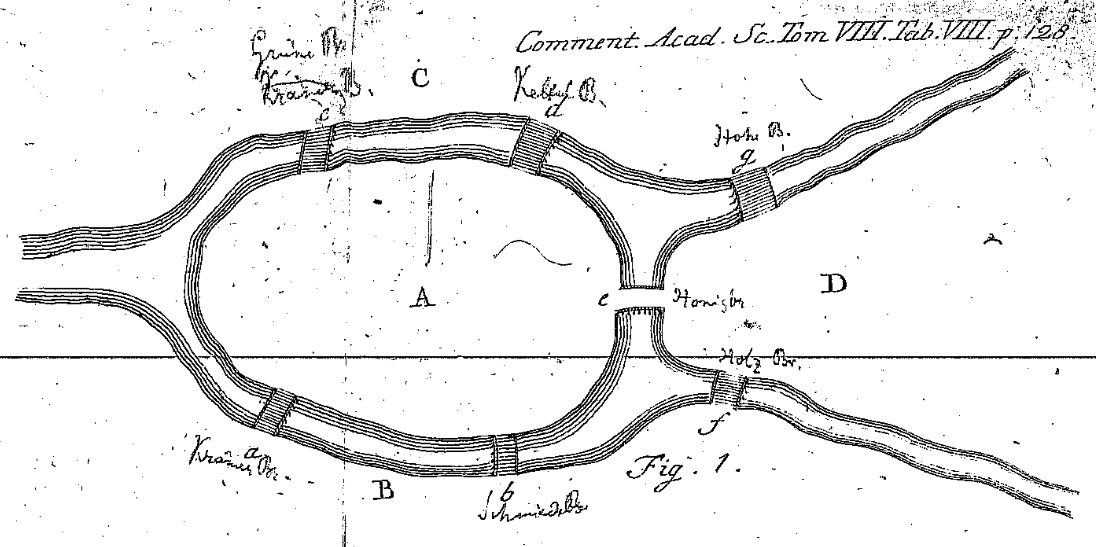
The kind of mathematics that Euler would have been familiar with - geometry - concerned notions of distance, area, and angles. Yet considering the problem of the bridges from a purely mathematical point of view, such quantities become irrelevant. The exact shape that the river takes and the distance between bridges are relevant to the individual planning on spending an afternoon walking over them, but less so to the mathematician. Indeed, the relevant information can be reduced to a list of the distinct land masses, and the bridges they connect. In modern terminology the problem can be redrawn as a graph:
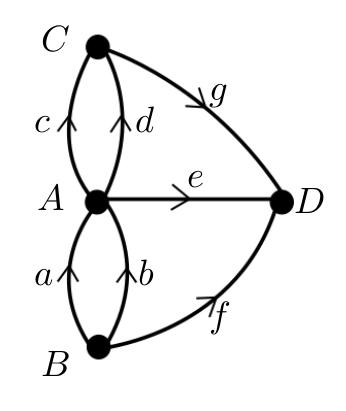
Each land mass is now represented by a vertex and each bridge is now an edge joining the corresponding vertices. We might say that the graph is topologically equivalent to the original diagram of the river and the bridges. I have labelled the vertices according to how Euler labelled them in his previous diagram. I have also added arrows indicating an orientation of the edges. Graphs are now ubiquitous in mathematics and science, and topology is only one perspective of study. You should not equate the graph with the way that it has been drawn above. The same graph could be drawn in many ways:
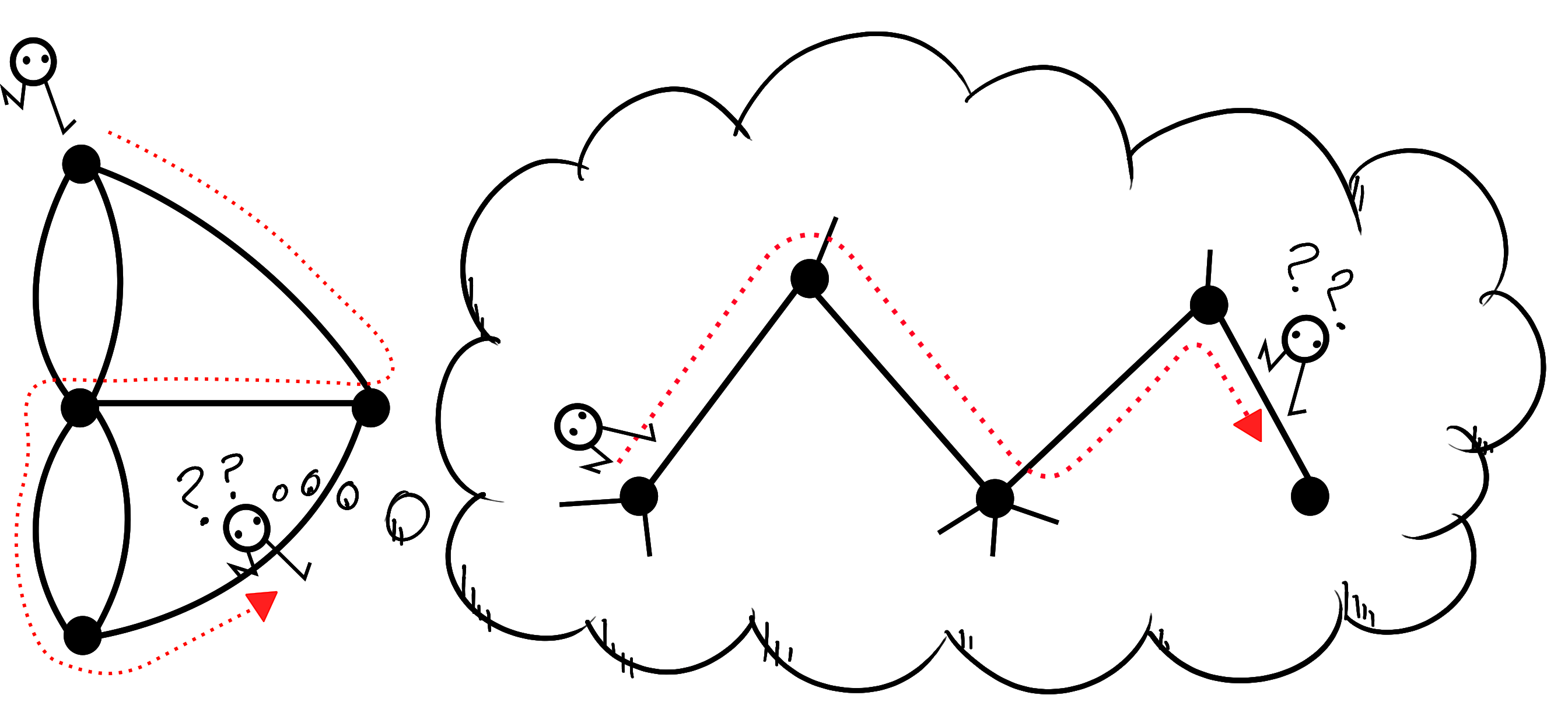
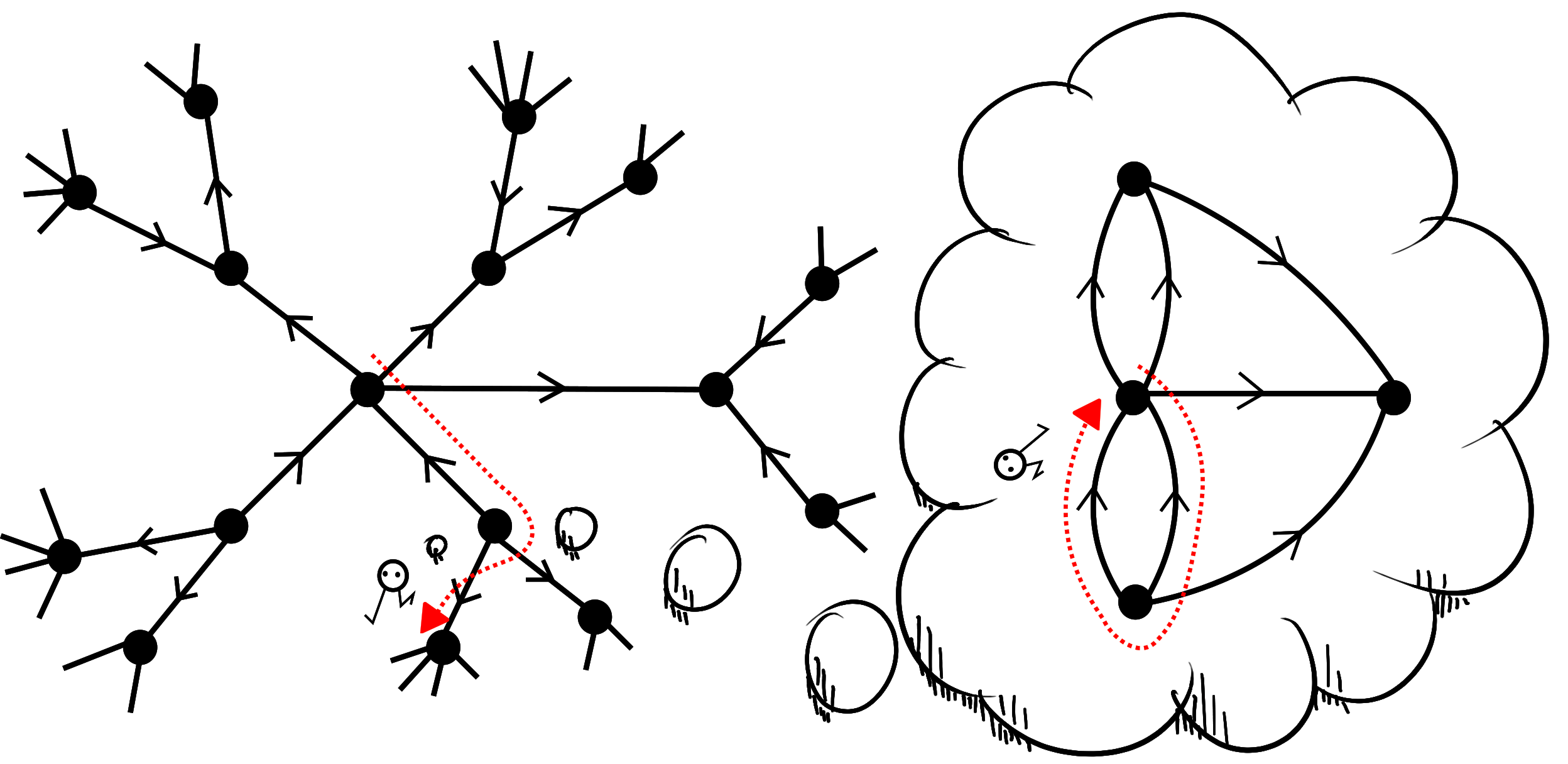
Let us now move on from Euler's problem and take the topological perspective one step further. We imagine the wanderer of the city is now a wanderer of our graph instead. They travels from vertex to vertex via the edges. Suppose that our wander has no map of the world they are living in. That is to say the wanderer has no idea what graph they are wandering around; whichever vertex they have arrived at, all they can see are the edges immediately connected to the vertex on which they stand. They can remember the route that they travelled to get there, but no more. Frustratingly, since we are now in a graph, and not the city of Königsberg, there are no landmarks with which the wanderer can orient themselves. If they return to a vertex they have no way of knowing. As we look down on our wanderer we can see exactly where they are, while they remain completely unaware. We can also take a look at the graph as they imagine it:
In the wanderer's imagination, how do they envision the graph? Since they never know if they have arrived at a vertex they have previously visited (without doubling back on themselves) this graph cannot contain any closed cycles - a path the begins and ends at the same vertex without repeating any other edge or vertex. A graph that does not contain any closed cycles is called a tree.
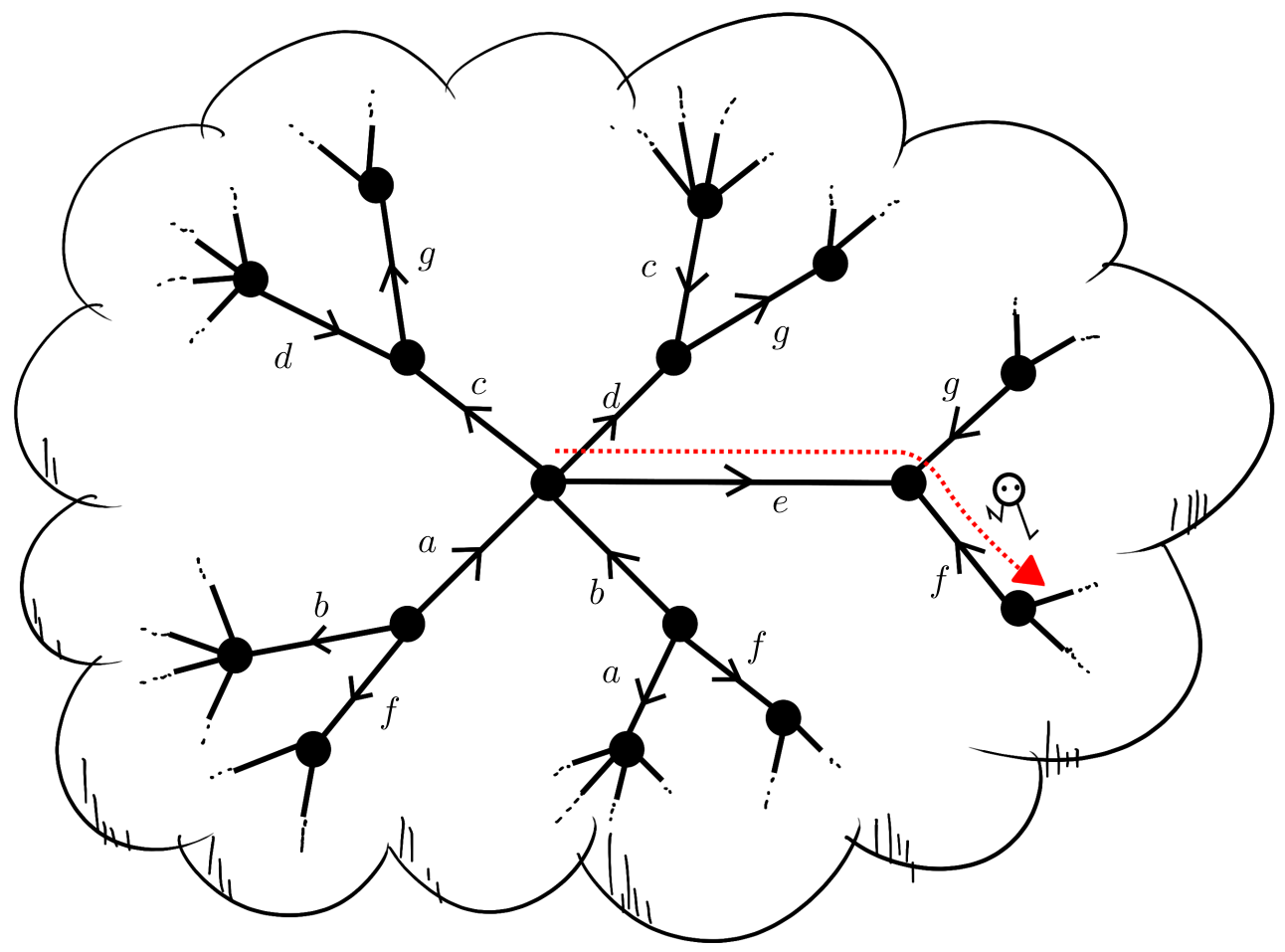
This tree, let's call it $\widetilde X$, is labelled in the picture according to which edge in $X$ it really corresponds to. These labels are invisible to our wanderer - if the labels were known then they could deduce what graph they were wandering about on. There is one particularly important vertex in $X$ and $\widetilde{X}$: the point at which our wanderer begins their journey, which we call the basepoint. This mapping between the graph $X$ and the universal cover $\widetilde X$ is usually written as a function $\widetilde X \rightarrow X$. The important feature here is that given a path that our wanderer takes in $X$, we can track the path they imagine they are taking in $\widetilde X$. Conversely, given a path in $\widetilde X$, using the labelling that only we can see, we can deduce the path that our wanderer has taken in $X$.
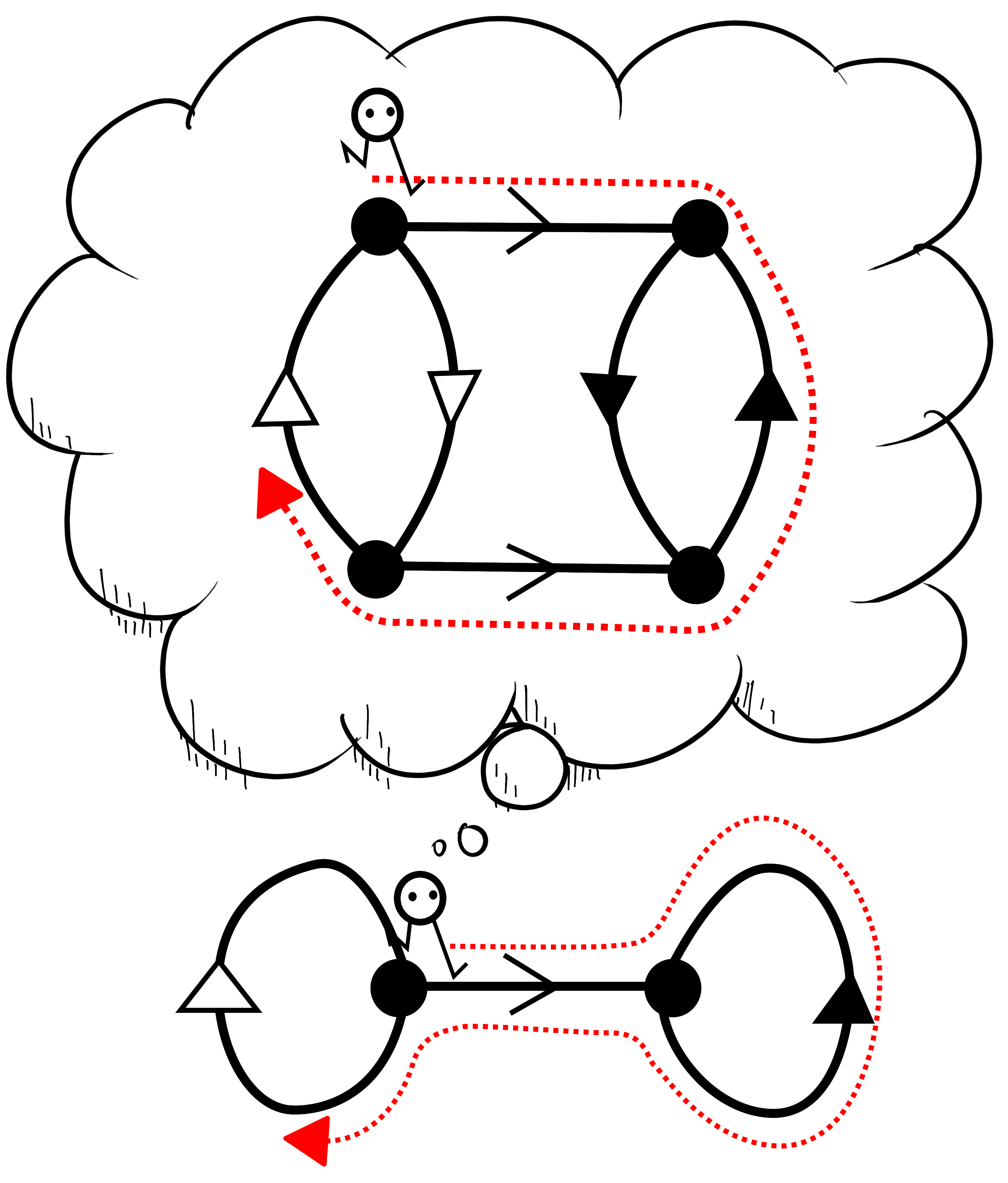
It is impossible for our wanderer to deduce what the graph $X$ is from $\widetilde X$. This is because $X$ isn't the only graph with universal cover $\widetilde X$. Setting aside Königsberg for a moment, consider the following graphs:
These graphs are obviously distinct, just by counting the vertices. But to a wanderer of these graphs, all they know is that whatever edge they choose to wander down, they will arrive at a vertex incident to precisely three edges. Wherever they go, the world to them looks exactly the same. There is no way for them to deduce if they are living in $X_1$, $X_2$, or $X_3$. Another way to say this is that $X_1$, $X_2$, and $X_3$ have the same universal cover $T_3$ - the 3-valent tree.
This isn't all that our wanderer could imagine. In principle they could try imagining that they are wandering around any graph we like. But that imagined graph should at least be consistent with what they actually experience. You can't arrive at a vertex with three incident edges but imagine there are four incident edges - that would present a contradiction to our wanderer and the illusion would be ruined. As a simple example, consider the reverse situation to the above: suppose our wanderer imagines they are navigating the Königsberg graph $X$, but in reality they are inside $\widetilde X$:
Provided that the basepoints match up as before, the wanderer would encounter no contradiction between what they are imagining and what they actually experience. But the situation would be particularly deceptive: as depicted above, our wanderer could imagine that they had walked a closed loop, when in fact they had not. This misconception is particularly bad for topologists, so we rule them out. Imagined graphs that do not cause the misconception are called covers, and there exist many of them aside from the universal cover. This definition for a cover is quite confusing, which is why we usually work with an equivalent and more practical condition in terms of labelling the edges of the cover according to the corresponding edges in the original graph. For example:
Note also that the cover given above is finite, while the universal cover is infinite. Unless the graph $X$ is itself a tree, the universal cover will always be infinite. Indeed, if $X$ is not a tree, then there is a closed cycle that our wanderer can walk around indefinitely, quite unaware that they are trapped in a closed loop.
A large part of my research is focused on the the following theorem:
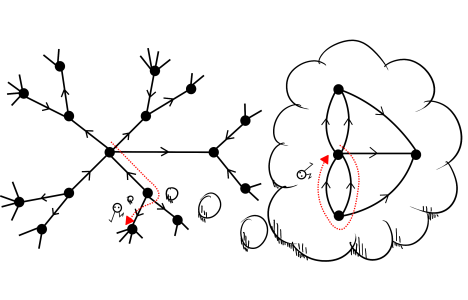
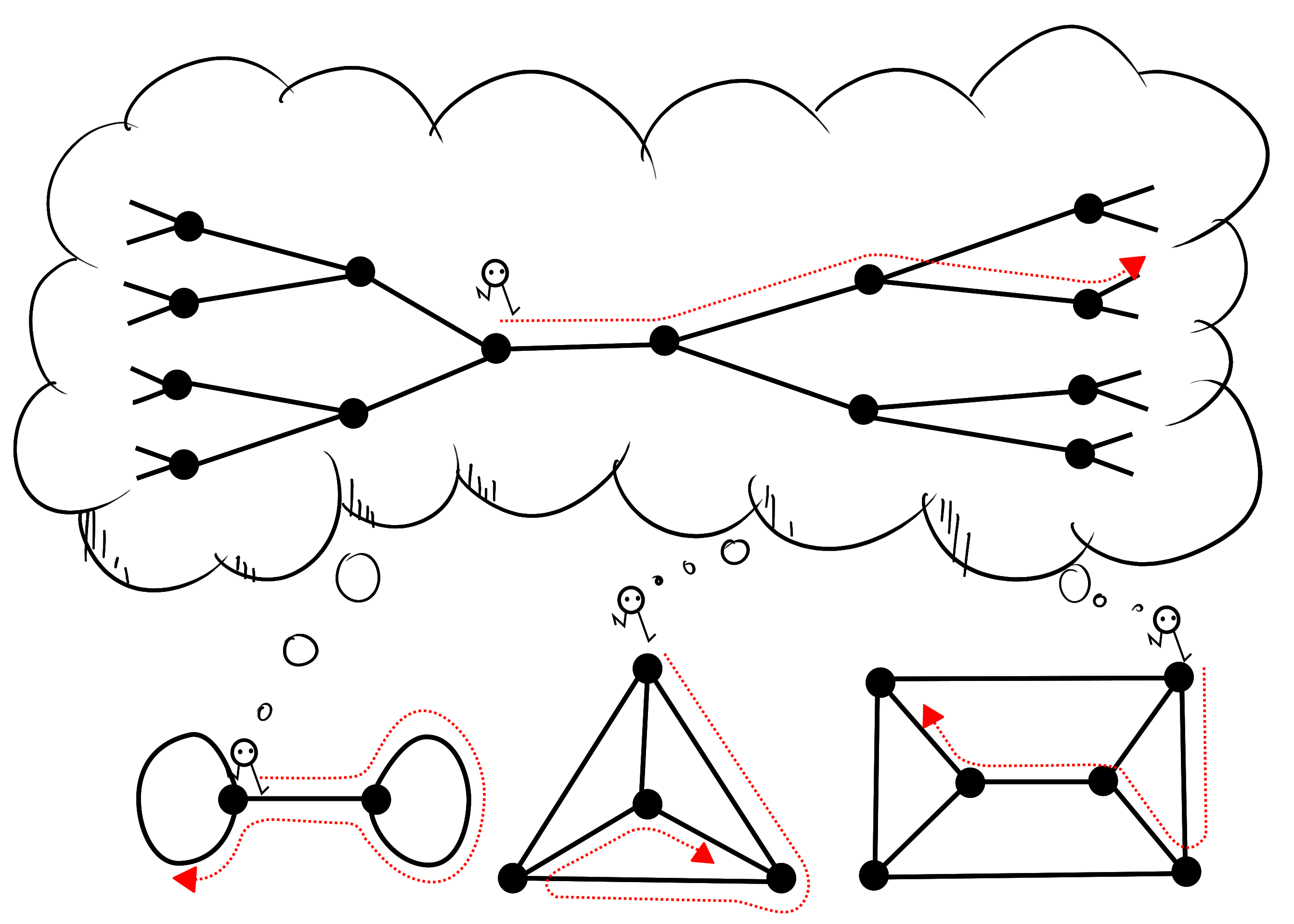
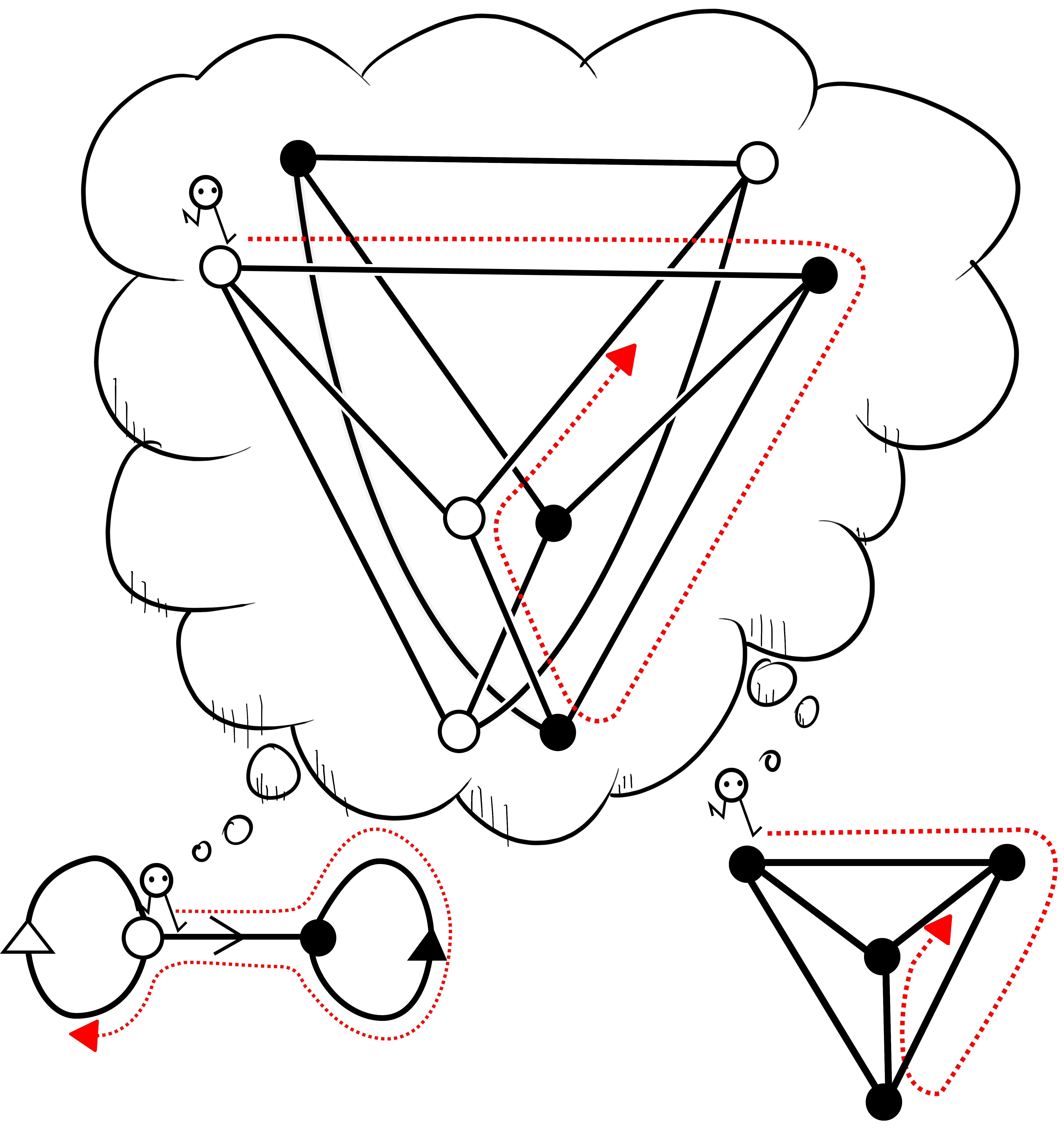
Theorem: Let $X_1$ and $X_2$ be finite graphs that have the same universal cover. Then they have a common finite cover.
Here is a picture of two wanderers living on two graphs with the same universal cover, imagining that they are living on a common cover:
This theorem was conjectured in an 1980 paper by the computer scientist Dana Angluin. Angluin was interested in distributed systems, which you can imagine as being a graph with a computer at each vertex and each edge corresponding to a 'port' connecting the neighbouring computers, allowing them to communicate. If this picture seems familiar that is because the internet is an example. The first complete proof of this theorem was given in a 1982 paper by Frank Thomas Leighton. Leighton is also a computer scientist and most of his research in graph theory was closely related to similar applications in computer science. The kind of problems that concerned Angluin and Leighton more closely resemble the kind of problem that Euler was considering than my own research. On the strength of the insights graph theory offers, Leighton co-founded Akamai Technologies in 1998, and today they are one of the internet's largest content delivery networks. He also retains an affiliation as a professor of applied mathematics at MIT and I have been told he still teaches an occasional course (I have the same teaching obligations as a billionaire, it turns out).
My own research has involved applying Leighton's theorem to the field of geometry and topology. Leighton's original proof was very much the argument of a computer scientist, and finding a new proof that offered a different theoretical framework has allowed me to solve previously unapproachable problems. There are two goals: the first is to generalise the theorem to higher dimensional topological spaces; and the second is to apply the generalisations to topological spaces or groups that decompose into a graph like structure. For example, in a recent preprint with fellow Oxford Mathematician Sam Shepherd we are able to prove quasi-isometric rigidity for a large family of hyperbolic groups. There are close connections to the theory of $3$-manifolds, their JSJ decompositions, and the recent resolution of the virtual Haken conjecture. In particular I believe that the right setting to generalise Leighton's theorem is special cube complexes."