Oxford Mathematcian Clemens Koppensteiner talks about his work on the geometry and topology of compactifications.
"It is not much of an exaggeration to say that in geometry all of the most beautiful and powerful statements we make are about compact spaces, i.e., spaces where all "points at infinity" are included. For example, one of Euclid's postulates (dealing with non-compact space) states that any two non-identical lines meet in exactly one point - except when they are parallel. On the other hand, in projective geometry (dealing with compact space) one has the much more satisfactory statement that any two non-identical lines meet in exactly one point - no exceptions needed.
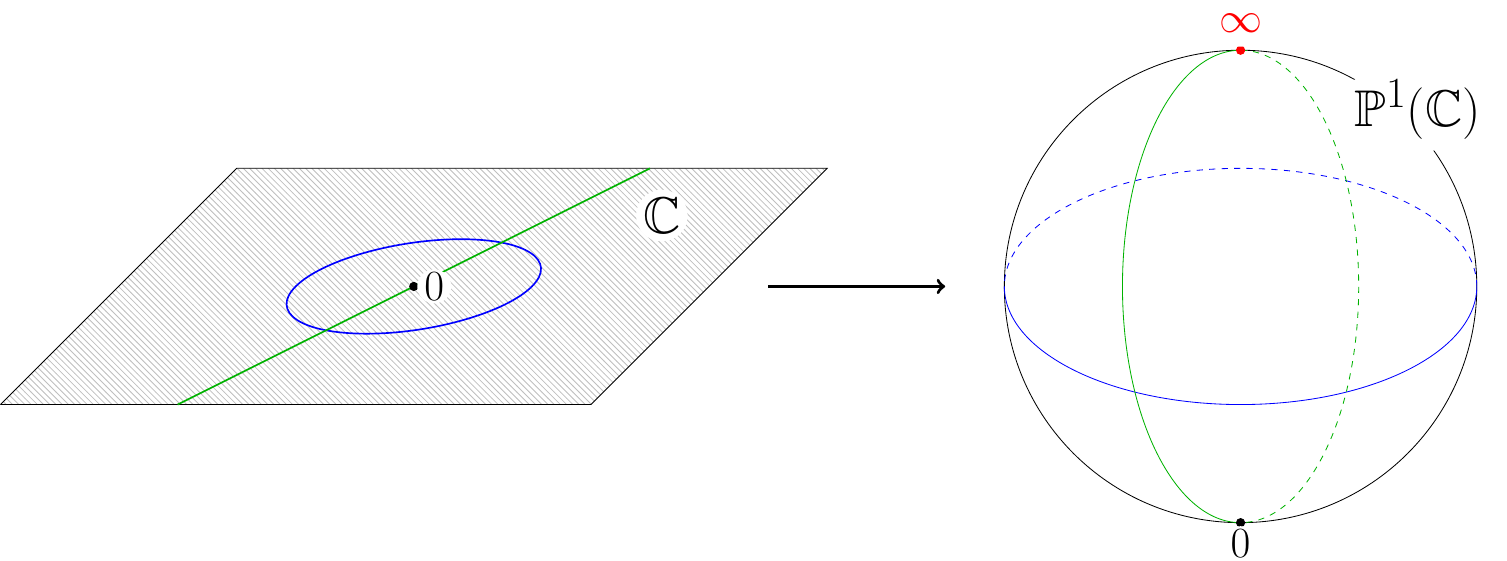
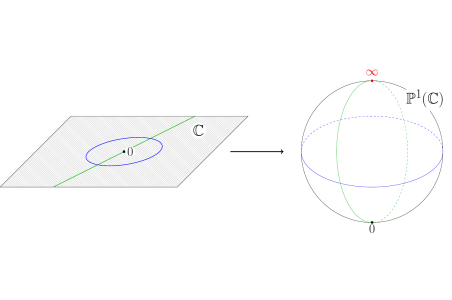
Image above: the complex plane can be compactified by wrapping it around a sphere and adding a point at the infinity at the north pole. The unit circle gets identified with the equator, while straight lines through the origin become meridians going through the new point $\infty$. The result is called the Riemann sphere.
For this reason, when making geometric arguments we often have to replace a non-compact space (say, the Euclidean plane) by a compact space (say, the projective plane) in a process called compactification. We then apply our powerful theorems to the compact space, and in the end restrict back to the original non-compact space.
When we are moreover interested in objects "living" on our spaces (e.g., functions, vector bundles or sheaves), we need to understand how these objects interact with the chosen compactification. In particular, we need a way to extend these objects to the new "points at infinity" in a controlled way.
In my research, I am particularly interested in objects with a notion of differentiation. Basic examples would be sets of functions, but usually I am working with vector bundles with a connection and their generalizations to D-modules. However, even for functions there are many "nonstandard" ways to differentiate them. For example, if $f(z)$ is function on the complement of the origin and $\lambda$ is any fixed number, we could set
\[
\frac{\mathrm{d}}{\mathrm{dz}} f(z) := f'(z) + \frac{\lambda}{z}f(z).
\]
One quickly checks that this definition still satisfies a version of the product rule and hence may really be called a type of "differentiation". If we now want to extend this differentiation rule to the origin, we run into the problem that $\frac{1}{z}$ does not make sense for $z=0$. One thus has to extend such a differentiation rule to so-called logarithmic connections, that is functions (or more generally vector bundles) with an action of the logarithmic differential operator $z\frac{\mathrm{d}}{\mathrm{d}z}$:
\[
z\frac{\mathrm{d}}{\mathrm{dz}} f(z) := zf'(z) + \lambda f(z).
\]
The term "logarithmic" comes from the fact that $z\frac{\mathrm{d}}{\mathrm{d}z}$ is dual to the logarithmic differential $\mathrm{d}\log z = \frac{\mathrm{d}z}{z}$.
Objects with a rule of differentiation arise in many contexts, so as mathematicians we want to classify them. Restricting to complex manifolds (or complex algebraic varieties), this is done by the famous Riemann-Hilbert correspondence: integrable connections (resp. regular holonomic D-modules) are the same as local systems (resp. perverse sheaves) on the manifold. Here one might think of "integrable connections" as collections of twisted higher-dimensional functions with differentiation and "regular holonomic D-modules" as everything that can be obtained from integrable connections under certain natural operations. Local systems and perverse sheaves are objects describing the topology of the manifold. The Riemann-Hilbert correspondence is quite miraculous: it builds a bridge between the (very rigid) geometry of complex manifolds and the (very flexible) underlying topology of the manifold.
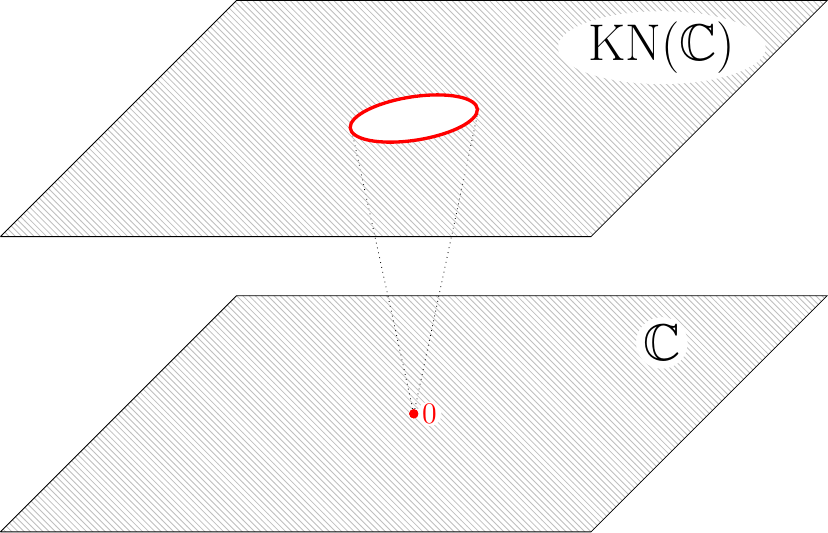
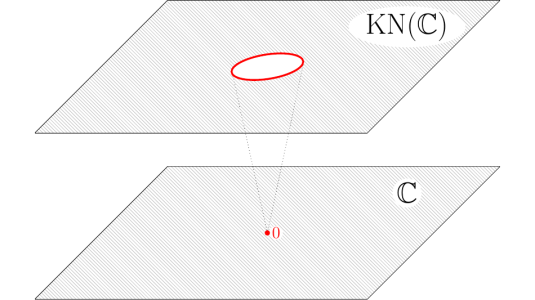
Image above: The Kato--Nakayama space of the plane replaces the origin by a circle. Each point of the added circle corresponds to a direction starting at the origin. One calls $\mathrm{KN}(\mathbb{C})$ the oriented real blow-up of the plane at the origin. In higher dimensions the topology becomes more complicated.
The corresponding theorem for logarithmic connections is more intricate: the geometry of the compactification turns out to be related to the topology of an auxiliary space, called the Kato-Nakayama space after its inventors. A full classification for logarithmic connections was achieved by Ogus. However, the classification of "regular holonomic logarithmic D-modules" is still open - in fact until recently it was not even known what such a thing should really be (despite logarithmic D-modules already being used in the 80s). A solution to this classification problem will also finally shed light on the old question of how to correctly understand the topology of compactifications.
In a series of papers we are building a theory of logarithmic D-modules ready for applications and work towards the following logarithmic Riemann-Hilbert conjecture.
Conjecture: The logarithmic de Rham functor $\widetilde{DR}_X$ gives an equivalence between the derived category of regular holonomic D-modules on a smooth log variety $X$ and a derived category of "constructible sheaves" on the Kato-Nakayama space of $X$, such that the following properties hold:
- The equivalence extends Ogus's Riemann-Hilbert correspondence for integrable log connections and reduces to the classical Riemann-Hilbert correspondence when the log structure is trivial.
- $\widetilde{DR}_X$ sends the standard t-structure to a perverse t-structure.
- There is a theory of singular support for constructible sheaves on the Kato-Nakayama space and it matches the theory of characteristic varieties for coherent log D-modules via the de Rham functor.
- Holonomic log D-modules have a natural filtration, which agrees with the Kashiwara-Malgrange V-filtration whenever the latter is defined. The de Rham functor matches this filtration with the intrinsic grading of constructible sheaves on the Kato-Nakayama space."
References:
Kato, K., Nakayama, C., Log Betti cohomology, log étale cohomology, and log de Rham cohomology of log schemes over $\mathbb{C}$. Kodai Math. J. 22 (1999), no. 2, 161-186.
Koppensteiner, C., Talpo, M., Holonomic and perverse logarithmic D-modules. Adv. Math. 346 (2019), 510-545.
Koppensteiner, C., The de Rham functor for logarithmic D-modules. Selecta Math. (N.S.) 26 (2020), no. 3, Paper No. 49.
Ogus, A., On the logarithmic Riemann-Hilbert correspondence. Doc. Math. 2003, Extra Vol. Kazuya Kato's fiftieth birthday, 655-724.